Как искать производную
- Дифференцирование функций: основы математического анализа
- Определение производной и ее связь с изменением функции
- Производная функции и ее связь с производной
- Вычисление производной
- Табличные производные и их использование
- Производные тригонометрических функций и их связь
- Свойства производных и их применение
- Производные сложных функций
- Вторая производная и ее вычисление
Дифференцирование функций: основы математического анализа
Дифференцирование функций является одной из основных концепций математического анализа. Оно позволяет находить производные функций и определять их скорость изменения в конкретной точке. Дифференцирование имеет большое значение не только в математике, но и в физике и других науках, которые изучают процессы.
Определение производной и ее связь с изменением функции
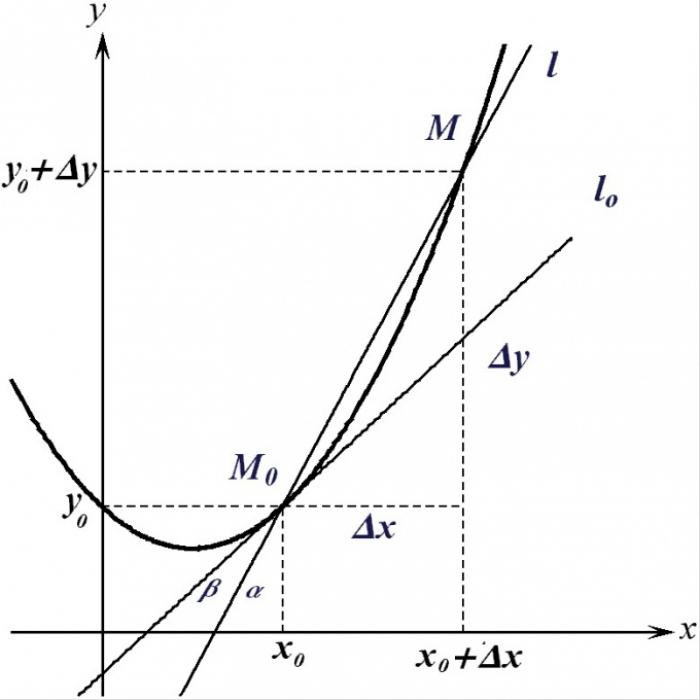
Производная функции f(x) в точке x0 определяется как предел отношения приращения этой функции к приращению ее аргумента, когда приращение аргумента стремится к нулю. Производная фактически показывает скорость изменения функции в данной точке. В математике приращения обычно обозначаются символом ∆. По определению, приращение функции ∆y = f(x0 + ∆x) - f(x0). Тогда производная равна f′(x0) = lim(∆y/∆x), ∆x → 0 = ∂y/∂x. Здесь символ ∂ обозначает бесконечно малое приращение или дифференциал.
Производная функции и ее связь с производной
Функция g(x), для которой в любой точке x0 ее области определения g(x0) = f′(x0), называется производной функцией или просто производной, и обозначается f′(x).
Вычисление производной
Для вычисления производной заданной функции можно использовать ее определение и вычислить предел отношения (∆y/∆x). Часто удобно преобразовать это выражение, чтобы можно было просто опустить ∆x. Например, если необходимо найти производную функции f(x) = x^2, можно выразить приращение ∆y = (x + ∆x)^2 - x^2 = 2x∆x + ∆x^2. Тогда предел отношения ∆y/∆x равен пределу выражения 2x + ∆x. Очевидно, что при ∆x → 0 это выражение стремится к 2x. Таким образом, (x^2)′ = 2x.
Табличные производные и их использование
Некоторые производные являются базовыми и легко вычисляются непосредственно. При решении задач на нахождение производных всегда полезно сводить заданную производную к табличным. Например, производная любой константы всегда равна нулю: (C)′ = 0. Для функции x^p, где p > 0, производная равна p*x^(p-1). Если p < 0, то (x^p)′ = -1/(p*x^(p+1)). Например, (x^4)′ = 4x^3, а (1/x)′ = -1/(x^2).
Производные тригонометрических функций и их связь
Производные тригонометрических функций связаны между собой следующим образом: (sin(x))′ = cos(x), (cos(x))′ = -sin(x).
Свойства производных и их применение
Производная суммы функций равна сумме производных: (f(x) + g(x))′ = f′(x) + g′(x). Если u(x) и v(x) — функции с производными, то (u*v)′ = u′*v + u*v′. Например, (x*sin(x))′ = x′*sin(x) + x*(sin(x))′ = sin(x) + x*cos(x). Производная от частного u/v равна (u′*v - u*v′)/(v^2). Например, если f(x) = sin(x)/x, то f′(x) = (sin(x) - x*cos(x))/(x^2). Свойство производной от константы заключается в следующем: если k — константа, то (k*f(x))′ = k*f′(x).
Производные сложных функций
Если дана функция, которую можно представить в виде f(g(x)), то f(u) называется внешней функцией, а u = g(x) — внутренней. Тогда f(g(x))′ = f′(g(x))*g′ (x). Например, если дана функция f(x) = sin(x)^2, то f′(x) = 2*sin(x)*cos(x). В этом примере квадрат является внешней функцией, а синус — внутренней. С другой стороны, sin(x^2)′ = cos(x^2)*2x. В этом примере синус — внешняя функция, а квадрат — внутренняя.
Вторая производная и ее вычисление
Также можно вычислить производную от производной, которая называется второй производной от f(x) и обозначается f″(x). Например, (x^3)″ = (3x^2)′ = 6x. Может существовать и производные более высоких порядков, такие как третья, четвертая и так далее.






