Как найти длину отрезка по координатам

- Три основные системы координат в геометрии и физике
- Декартова система координат
- Полярная система координат
- Сферическая система координат
- Вывод
Три основные системы координат в геометрии и физике
Существуют три основные системы координат, используемых в геометрии, теоретической механике и других разделах физики: декартова, полярная и сферическая. В каждой из этих систем каждая точка имеет три координаты.
Декартова система координат
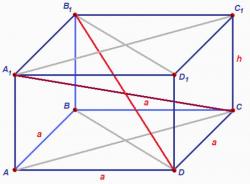
Декартова система координат является прямоугольной. Положение точки в этой системе координат определяется координатами x, y и z. Координаты точки являются проекциями радиус-вектора на координатные оси. Расстояние между двумя точками в декартовой системе координат может быть определено с использованием модуля вектора.
Полярная система координат
Полярная система координат состоит из радиальной координаты r, угловой координаты θ и координаты z, аналогичной координате z в декартовой системе. Полярные координаты могут быть переведены в декартовы координаты с использованием тригонометрических функций. Расстояние между двумя точками в полярной системе координат также может быть вычислено с помощью модуля вектора.
Сферическая система координат
Сферическая система координат включает в себя три координаты: расстояние от начала координат до точки (r), азимутальный угол (θ) и зенитный угол (φ). Координаты в сферической системе могут быть переведены в декартовы координаты с использованием тригонометрических функций. Расстояние между двумя точками в сферической системе координат также может быть определено с использованием модуля вектора.
Вывод
Три основные системы координат - декартова, полярная и сферическая - применяются в геометрии, теоретической механике и других разделах физики. Каждая система координат имеет свои преимущества и используется для определения положения точек и расстояния между ними. Понимание этих систем координат является важным для работы с пространственными данными и анализа физических явлений.