Как найти длину стороны треугольника
- Треугольник и его типы
- Вычисление сторон прямоугольного треугольника
- Вычисление сторон произвольного треугольника
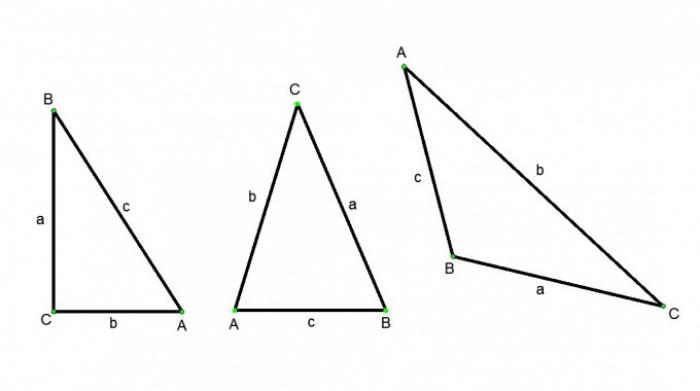
Треугольник и его типы
Треугольник – это фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков соединяющих эти точки попарно. Точки называются вершинами (обозначаются заглавными буквами), а отрезки сторонами (обозначаются малыми буквами) треугольника. Различают следующие типы треугольников: остроугольный треугольник (все три угла острые), тупоугольный треугольник (один из углов тупой), прямоугольный треугольник (один из углов прямой), равнобедренный (две его стороны равны), равносторонний (все его стороны равны).
Вычисление сторон прямоугольного треугольника
Инструкция 1 Соотношение сторон и углов в прямоугольном треугольнике:Пусть ABC – прямоугольный треугольник, угол С – прямой, углы A и B – острые. Тогда согласно определению косинуса: косинус угла A равен отношению прилежащего катета BC к гипотенузе AB. Синусом угла А называется отношение противолежащего катета BC к гипотенузе AB. Тангенсом угла А называется отношение противолежащего катета BC к прилежащему AC.Из данных определений получаем следующие соотношения:Катет, противолежащий углу А, равен произведению гипотенузы на синус А, или равен произведению второго катета на тангенс А;Катет, прилежащий к углу А, равен произведению гипотенузы на косинус А;В прямоугольном треугольнике любая из сторон может быть вычислена по теореме Пифагора, если известны две другие. Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Вычисление сторон произвольного треугольника
Инструкция 2 Соотношение сторон в произвольном треугольнике:Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.
Вывод: Вычисление сторон треугольника зависит от его типа и предоставленных данных. Для прямоугольного треугольника можно использовать теорему Пифагора и определения косинуса, синуса и тангенса углов. Для произвольного треугольника существуют теоремы косинусов и синусов, которые позволяют найти соотношения между сторонами и углами треугольника.