Как найти косинус в теореме косинусов
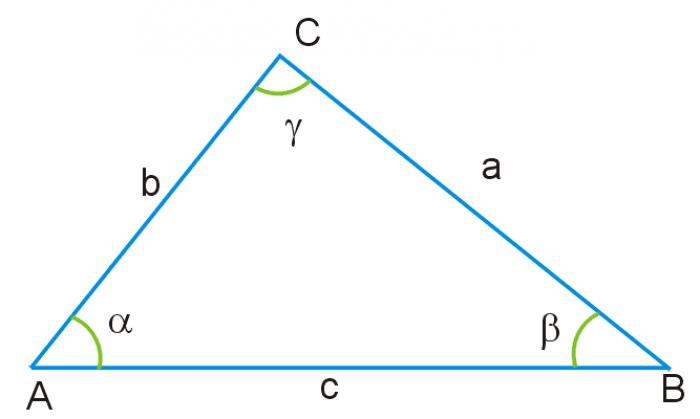
- Теорема косинусов: нахождение третьей стороны по углу и двум сторонам
- cosγ = √((b^2 + c^2 - a^2)/(2bc))
- Использование арккосинуса для нахождения углов треугольника
- Пример применения теоремы косинусов
- Таким образом, третья сторона треугольника примерно равна 4.984.
- Примечание по единицам измерения углов
Теорема косинусов: нахождение третьей стороны по углу и двум сторонам
Теорема косинусов в математике часто применяется для нахождения третьей стороны треугольника, когда известны угол и две стороны. Формула для этого выражается следующим образом:
a^2 = b^2 + c^2 - 2bc*cosγ, где a - третья сторона треугольника, b и c - известные стороны, γ - известный угол.
Использование теоремы косинусов для нахождения угла при известных трех сторонах
Иногда задача ставится наоборот: требуется найти угол при известных трех сторонах. Для этого мы можем использовать теорему косинусов и преобразовать формулу следующим образом:
cosγ = √((b^2 + c^2 - a^2)/(2bc))
Использование арккосинуса для нахождения углов треугольника
Чтобы найти углы треугольника при известных сторонах, мы можем использовать арккосинус - обратную тригонометрическую функцию. Арккосинус числа m определяет угол γ, при котором cosγ равен m. Функция arccos является убывающей функцией.
Пример применения теоремы косинусов
Допустим, у нас есть треугольник со сторонами b = 5, c = 7 и углом γ = 45°. Мы можем использовать теорему косинусов, чтобы найти третью сторону треугольника:
a^2 = 5^2 + 7^2 - 2*5*7*cos45°
a^2 = 25 + 49 - 70*cos45°
a^2 = 74 - 70*0.7071
a^2 = 24.8459
a ≈ 4.984
Таким образом, третья сторона треугольника примерно равна 4.984.
Примечание по единицам измерения углов
В случае использования радианов, углы могут быть переведены в градусы по следующему соотношению: π радиан = 180 градусов. При использовании инженерных калькуляторов, следует обратить внимание на возможность переключения единиц измерения углов.