Как найти периметр равнобедренной трапеции
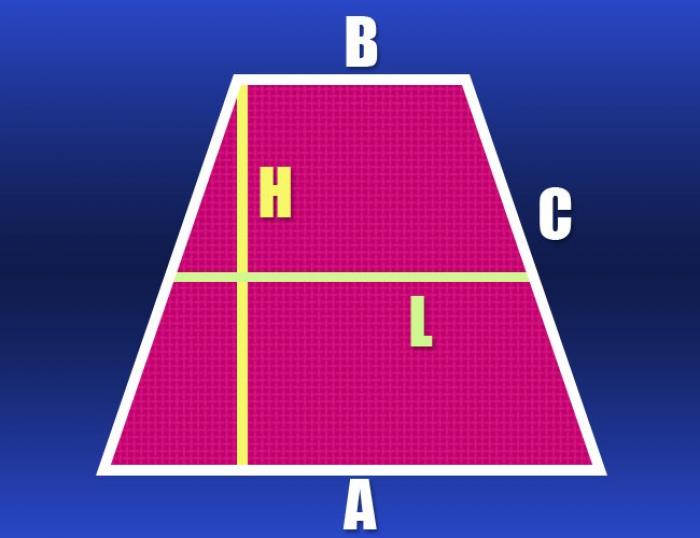
- Трапеция: определение и основные характеристики
- Периметр трапеции с известными сторонами
- Периметр трапеции с известной средней линией
- Периметр трапеции с известными основаниями и высотой
- Периметр трапеции с известным меньшим основанием и высотой
Трапеция: определение и основные характеристики
Трапеция - это двухмерная геометрическая фигура, которая имеет четыре вершины и только две параллельные стороны. В зависимости от свойств сторон и углов, трапеция может быть равнобедренной или равнобокой.
Периметр трапеции с известными сторонами
Если известны длины обоих оснований (a и b) и длина боковой стороны (c), то периметр (P) этой равнобедренной трапеции можно рассчитать по простой формуле: P = a + b + 2c.
Периметр трапеции с известной средней линией
Если длины обоих оснований трапеции неизвестны, но дана длина средней линии (l) и боковой стороны (c), то можно вычислить периметр (P) равнобедренной трапеции по формуле: P = 2l + 2c. Средняя линия параллельна обоим основаниям и равна их полусумме.
Периметр трапеции с известными основаниями и высотой
Если известны длины обоих оснований (a и b) и высота (h) равнобедренной трапеции, то можно восстановить длину недостающей боковой стороны. Для этого рассмотрим прямоугольный треугольник, в котором гипотенузой будет неизвестная сторона, а катетами - высота и короткий отрезок, который она отсекает от длинного основания трапеции. Длина этого отрезка равна половине разности между длинами большего и меньшего оснований: (a-b)/2. Длина гипотенузы (боковой стороны трапеции), согласно теореме Пифагора, будет равна квадратному корню из суммы квадратов длин обоих катетов. Заменяя в формуле из первого шага длину боковой стороны на полученное выражение, получим формулу для вычисления периметра: P = a + b + 2√(h²+(a-b)²/4).
Периметр трапеции с известным меньшим основанием и высотой
Если в условиях задачи даны длина меньшего основания (b) и боковой стороны (c), а также высота (h) равнобедренной трапеции, можно вычислить длину катета во вспомогательном прямоугольном треугольнике. Воспользуемся теоремой Пифагора и найдем корень из разности между квадратом длины боковой стороны (гипотенузы) и квадратом высоты (катета): √(c²-h²). По этому отрезку неизвестного основания трапеции можно восстановить его длину, удвоив это выражение и добавив к результату длину меньшего основания: b+2√(c²-h²). Подставив это выражение в формулу из первого шага, получим формулу для вычисления периметра: P = b + 2√(c²-h²) + b + 2c = 2(√(c²-h²) + b + c).
Теперь, зная различные формулы для вычисления периметра равнобедренной трапеции в зависимости от доступных данных, вы сможете решать задачи по геометрии, связанные с этой фигурой.






