Как найти высоту в правильной пирамиде
- Высота пирамиды: определение и способы нахождения
- Способ 1: нахождение высоты через объем пирамиды
- Способ 2: нахождение высоты через теорему Пифагора
- Способ 3: пример нахождения высоты
Высота пирамиды: определение и способы нахождения
Пирамида - это многогранник, у которого в основании лежит многоугольник, а грани представляют собой треугольники, имеющие общую вершину. Правильная пирамида отличается тем, что в ее основании лежит правильный многоугольник. Высота пирамиды определяется как отрезок, проведенный от вершины пирамиды к основанию, и перпендикулярный ему. В этой статье мы рассмотрим несколько способов нахождения высоты пирамиды.
Способ 1: нахождение высоты через объем пирамиды
Один из способов нахождения высоты пирамиды - выразить ее через объем. Для этого используется формула:
V = (S*h)/3, где V - объем пирамиды, S - площадь всех боковых граней пирамиды в сумме, h - высота пирамиды.
Из этой формулы можно вывести другую, для нахождения высоты пирамиды:
h = (3*V)/S
Для примера, если известно, что площадь боковых граней пирамиды равна 84 см², а объем пирамиды составляет 336 куб.см, то высоту можно найти следующим образом:
h = (3*336)/84 = 12 см
Ответ: высота данной пирамиды равна 12 см.
Способ 2: нахождение высоты через теорему Пифагора
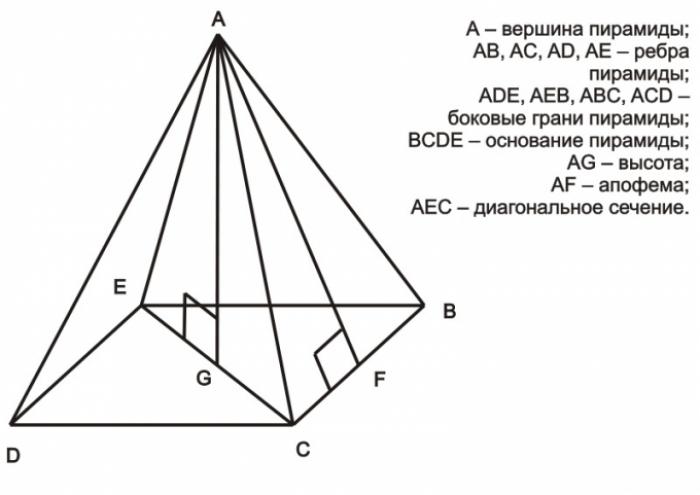
Рассматривая правильную пирамиду с правильным многоугольником в основании, можно использовать теорему Пифагора для нахождения высоты. В данном случае, треугольник, образованный высотой, половиной диагонали и одной из граней пирамиды, является прямоугольным треугольником.
Используя теорему Пифагора (a² = b² + c²), где a - гипотенуза, b - половина диагонали многоугольника в основании, c - высота пирамиды, можно выразить высоту следующим образом:
c = √(a² - b²)
Примером может служить треугольник AEG, где AE - грань пирамиды, EG - половина диагонали многоугольника в основании.
Способ 3: пример нахождения высоты
Для более наглядного примера нахождения высоты правильной пирамиды, рассмотрим следующую ситуацию: длина грани пирамиды составляет 12 см, а длина диагонали многоугольника в основании - 8 см.
Используя теорему Пифагора, можно записать уравнение: 12² = 4² + c², где c - неизвестный катет (высота) данной пирамиды (прямоугольного треугольника).
Решая уравнение, получим: 144 = 16 + c²
Отсюда следует, что высота данной пирамиды равна √128 или приблизительно 11.3 см.
Таким образом, нахождение высоты пирамиды может быть достигнуто различными способами, в зависимости от известных данных и ситуации. Это позволяет более точно определить геометрические характеристики пирамиды и использовать их при решении задач и расчетах.