Как определить чётную функцию
- Определение чётных и нечётных функций
- Определение чётной функции
- Пример чётной функции
- График чётной функции
- Симметричность графика чётной функции
- Не каждая функция является чётной или нечётной
- Утверждения для исследования функций на чётность
- Простой способ определения чётности функции
Определение чётных и нечётных функций
Чётные и нечётные функции – это числовые функции, области определения которых симметричны относительно системы координат. Для определения чётности функции, нужно запомнить её определение. Функцию f (x) можно назвать чётной, если для любого значения x из области определения выполняются два равенства: а) -x € D; б) f (-x) = f (x).
Определение чётной функции
Для определения чётной функции, нужно запомнить, что если при противоположных значениях x значения y равны, то исследуемая функция является чётной.
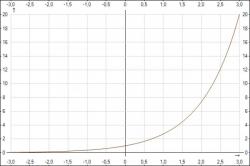
Пример чётной функции
Рассмотрим функцию y = x?. При значении x = -3, y = 9, и при противоположном значении x = 3 y = 9. Обратите внимание, данный пример доказывает, что при противоположных значениях x значения y равны.
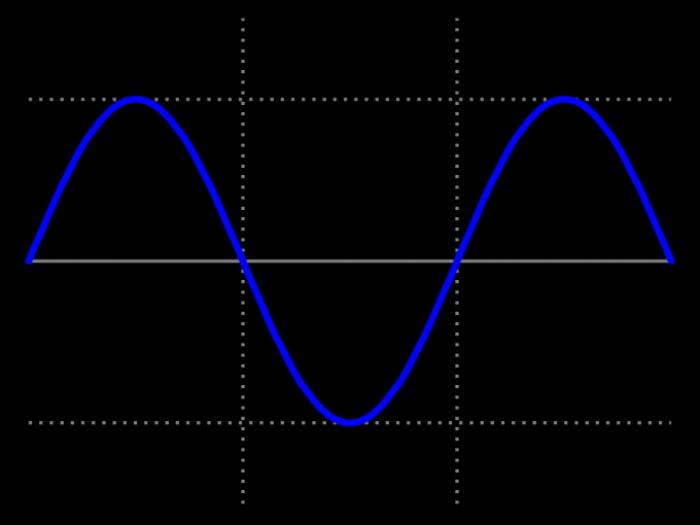
График чётной функции
На всей области определения график чётной функции симметричен оси OY. Простейшим примером чётной функции служат функции y = cos x; y = ?x?; y = x? + ?x?.
Симметричность графика чётной функции
Если точка (a; b) принадлежит графику чётной функции, то и симметричная ей относительно оси ординат точка (-a; b) также принадлежит данному графику, из чего следует, что график чётной функции симметричен относительно оси ординат.
Не каждая функция является чётной или нечётной
Не каждая функция обязательно является либо чётной, либо нечётной. Некоторые функции могут быть суммой чётной и нечётной функций (примером может служить функция f (x) = 0).
Утверждения для исследования функций на чётность
При исследовании функции на чётность, нужно запомнить следующие утверждения: а) сумма чётных (нечётных) функций также является чётной (нечётной) функцией; б) произведение двух чётных или нечётных функций является чётной функцией; в) произведение нечётной и чётной функций является нечётной функцией; г) если функция f чётна (либо нечётна), то и функция 1/f также является чётной (либо нечётной).
Простой способ определения чётности функции
Функция называется чётной, если при изменении знака аргумента значение функции остаётся неизменным. Используйте этот простой способ для определения чётности функции: если значение останется неизменным при умножении на -1, то функция – чётная.