Как построить логарифмическую функцию
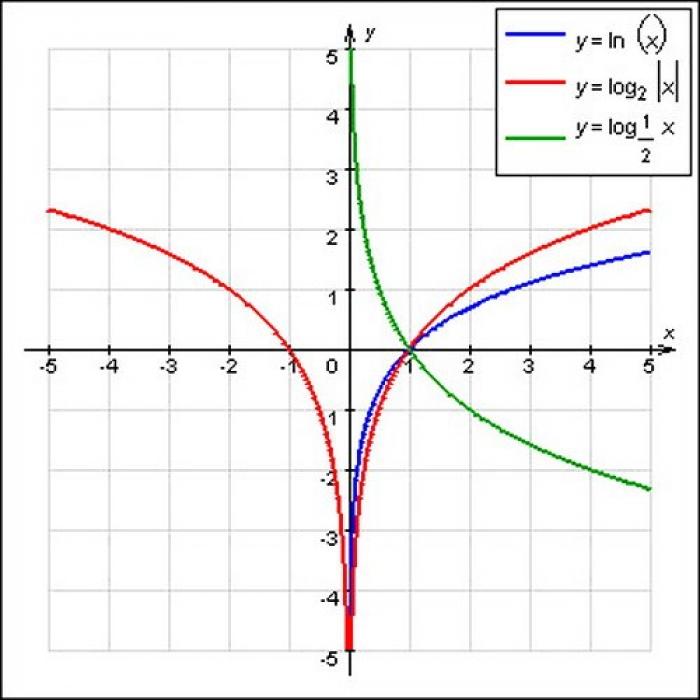
- Построение графика логарифмической функции
- Необходимые материалы
- Инструкция
- Построение графика
- Для построения графика функции y = logax следуйте следующим шагам:
- Важное замечание
- Полезный совет
Построение графика логарифмической функции
Логарифмической называется функция, которая обратна показательной. Такая функция имеет вид: y = logax, в которой значение a – положительное число (не равное нулю). Внешний вид графика логарифмической функции зависит от значения a.
Необходимые материалы
Для построения графика логарифмической функции вам понадобятся следующие материалы:
- Математический справочник
- Линейка
- Простой карандаш
- Тетрадь
- Ручка
Инструкция
Прежде чем приступить к построению графика логарифмической функции, обратите внимание на следующие моменты:
- Областью определения данной функции является множество положительных чисел (R+), в то время как областью значения являются действительные числа.
- Если значение a больше 1, то на графике будет изображена возрастающая логарифмическая функция. Для доказательства этого факта можно использовать метод от противного.
- Предположим, что loga x2≤loga x1. Учитывая то, что показательная функция вида у=ах при значении а>1 возрастает, получим неравенство aloga x2≤aloga x1. По определению логарифма aloga x2=x2, в то время как aloga x1=x1. Таким образом, неравенство приводит к x2≤x1, что противоречит начальным допущениям x2>x1. Следовательно, при a>1 логарифмическая функция возрастает.
Построение графика
Для построения графика функции y = logax следуйте следующим шагам:
- График функции будет проходить через точку (1;0).
- Если значение a>1, то функция будет возрастающей.
- Для точности построения графика рассчитайте значения y при различных значениях x (например, 0.5, 2, 4, 8). На основании этих данных поставьте точки и постройте график.
Важное замечание
Если в задании логарифм обозначен как lg x, не думайте, что это ошибка. Такое обозначение означает десятичный логарифм.
Полезный совет
Для повышения точности построения графика логарифмической функции рекомендуется рассчитать значения y при различных значениях x (например, 0.5, 2, 4, 8). Затем, используя эти данные, поставьте точки на графике и соедините их, чтобы получить график функции.






