Как решать логарифмическое неравенство

Содержание:

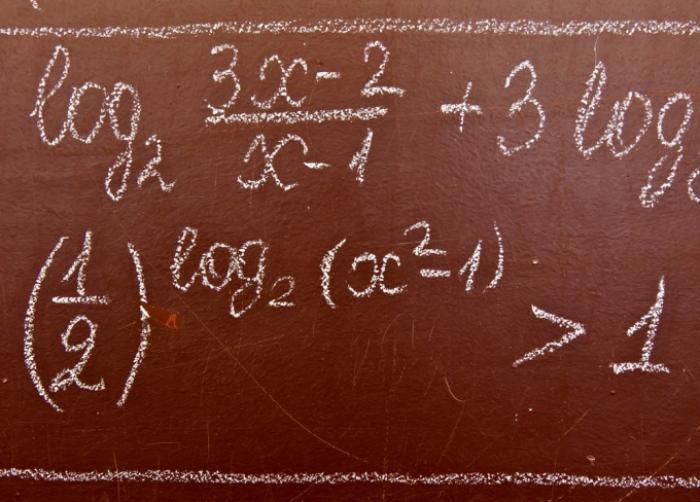
1. Логарифмические неравенства: основные утверждения и примеры решений
2. Утверждение 1: неравенства с положительным основанием логарифма
3. Утверждение 2: неравенства с основанием логарифма от 0 до 1
4. Рассмотрим пример:
5. Специальные случаи и замена переменной
6. Дополнительная информация

Логарифмические неравенства: основные утверждения и примеры решений

Логарифмические неравенства - это неравенства, в которых присутствуют неизвестные под знаком логарифма или в его основании. Для решения таких неравенств применяются определенные методы и утверждения.

Утверждение 1: неравенства с положительным основанием логарифма

Если основание логарифма а > 0, то неравенство logaF(x) > logaG(x) эквивалентно системе неравенств F(x) > G(x), F(x) > 0, G(x) > 0. Рассмотрим пример:

У нас есть неравенство lg(2x^2+4x+10) > lg(x^2-4x+3). Перейдем к равносильной системе неравенств: 2x^2+4x+10 > x^2-4x+3, 2x^2+4x+10 > 0, x^2-4x+3 > 0. Решив эту систему, мы получим решение исходного неравенства: x принадлежит интервалам (-бесконечность, -7), (-1, 1), (3, +бесконечность).

Утверждение 2: неравенства с основанием логарифма от 0 до 1

Если основание логарифма находится в интервале от 0 до 1, то неравенство logaF(x) > logaG(x) эквивалентно системе неравенств F(x) > 0, G(x) > 0. Например:

Пусть log(x+25) по основанию 0.5 > log(5x-10) по основанию 0.5. Перейдем к равносильной системе неравенств: x+25 < 8x-10, x+25 > 0, 8x-10 > 0. Решив эту систему неравенств, мы получаем x > 5, что и является решением исходного неравенства.

Утверждение 3: неравенства с неизвестным под знаком логарифма и в его основании

Если неизвестное одновременно стоит под знаком логарифма и в его основании, то уравнение logF(x) по основанию h(x) > logG(x) по основанию h(x) эквивалентно совокупности систем:

1) h(x) > 1, F(x) > G(x), F(x) > 0, G(x) > 0;
2) h(x) < 1, F(x) > G(x), F(x) > 0, G(x) < 0.

Рассмотрим пример:

Пусть log(5-x) по основанию (x+2)/(x-3) > log(4-x) по основанию (x+2). Применим равносильный переход к совокупности систем неравенств:
1) (x+2)/(x-3) > 1, x+2 > 4-x, x+2 > 0, 4-x > 0;
2) (x+2)/(x-3) < 1, x+2 < 4-x, x+2 > 0, 4-x < 0.

Решив данную совокупность систем, мы получаем определенное множество значений для x.

Специальные случаи и замена переменной

Некоторые логарифмические уравнения могут быть решены с помощью замены переменной. Например, уравнение (lgX)^2+lgX-2 >= 0 может быть заменено на t^2+t-2 >= 0, где t = lgX. Решая полученное уравнение, мы получаем определенные значения для t, которые затем преобразуются обратно в значения x.

Обратите внимание, что в утверждениях 1-3 могут присутствовать любые знаки (>=, <=, >, <).

Дополнительная информация

Логарифм с основанием 10 называется десятичным логарифмом и обозначается lgX. Логарифм с основанием 2.7 называется натуральным логарифмом и обозначается lnX. Они широко применяются в различных областях математики и науки.