Как решать матрицу по Гауссу

Содержание:

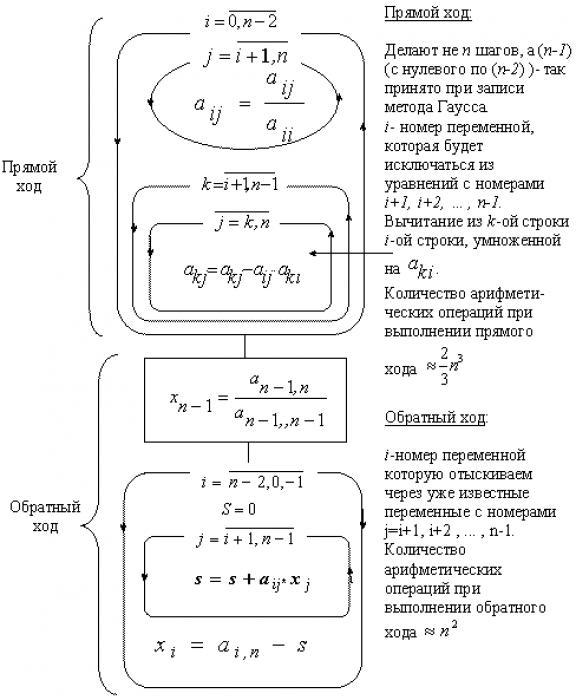
1. Метод Гаусса: основные принципы решения системы линейных уравнений
2. Прямой ход метода Гаусса
3. Обратный ход метода Гаусса
4. На следующем шаге выражаем базисные неизвестные через свободные.
5. Запись ответа в векторном или покоординатном виде
6. Использование программ для решения системы линейных уравнений

Метод Гаусса: основные принципы решения системы линейных уравнений

Метод Гаусса является одним из основных принципов решения системы линейных уравнений. Его преимущество заключается в том, что оно не требует квадратичности исходной матрицы или же предварительного расчета ее определителя. Для применения метода Гаусса вам понадобится учебник по высшей математике.

Прямой ход метода Гаусса

Прямой ход метода Гаусса состоит из нескольких шагов. Вначале необходимо записать систему линейных алгебраических уравнений в матричном виде. Затем следует составить расширенную матрицу и привести ее к ступенчатому виду с помощью элементарных преобразований строк. Матрица имеет ступенчатый вид, если выполняются два условия: все последующие строки являются нулевыми, если первая строка нулевая, и опорный элемент каждой последующей строки находится правее, чем в предыдущей. Элементарные преобразования строк включают перестановку местами строк, замену строки суммой этой строки с другой, умножение строки на число.

Определите ранг расширенной матрицы и сделайте вывод о совместности системы. Если ранг матрицы А не совпадает с рангом расширенной матрицы, то система несовместна и не имеет решения. Если же ранги совпадают, то система совместна, и можно продолжать поиск решений.

Обратный ход метода Гаусса

Обратный ход метода Гаусса начинается с объявления базисных неизвестных теми, чьи номера совпадают с номерами базисных столбцов матрицы А в ступенчатом виде. Остальные переменные считаются свободными. Число свободных неизвестных вычисляется по формуле k = n - r(A), где n - число неизвестных, r(A) - ранг матрицы А.

Далее возвращаемся к ступенчатой матрице и приводим ее к виду Гаусса. Ступенчатая матрица имеет вид Гаусса, если все опорные элементы равны единице, а над опорными элементами только нули. Затем записываем систему алгебраических уравнений, соответствующую матрице вида Гаусса, обозначив свободные неизвестные как C1, ..., Ck.

На следующем шаге выражаем базисные неизвестные через свободные.

Запись ответа в векторном или покоординатном виде

После выражения базисных неизвестных через свободные, записываем ответ в векторном или покоординатном виде в зависимости от поставленной задачи.

Использование программ для решения системы линейных уравнений

Существует множество программ, которые могут помочь в решении системы линейных уравнений. Если вас интересует именно ответ, а не механизм метода, то вполне можно воспользоваться ими. Однако, понимание метода Гаусса и его применение может быть полезным для изучения математических основ и получения глубокого понимания решения систем линейных уравнений.