Как составить уравнение окружности
- Окружность и её уравнение
- Уравнение окружности с центром в начале координат
- Уравнение окружности с произвольным центром
- Уравнение окружности через заданную точку
- Построение окружности
- Тригонометрическое представление окружности
- Обобщение уравнения окружности с произвольным центром
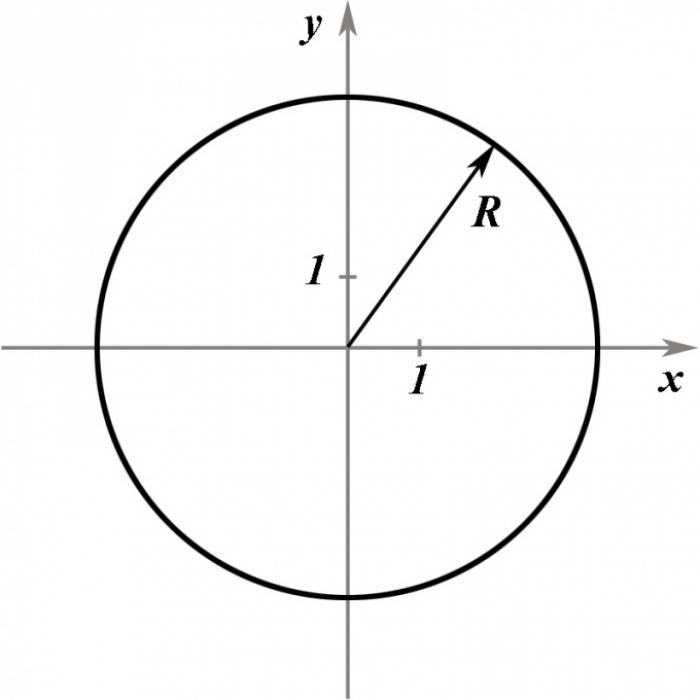
Окружность и её уравнение
Окружность - это совокупность точек, расположенных на одинаковом расстоянии от заданной точки, которая называется центром окружности. Уравнение окружности в декартовых координатах определяет все точки, которые лежат на окружности.
Уравнение окружности с центром в начале координат
Для составления уравнения окружности с центром в начале координат, нужно учесть, что окружность состоит из точек, находящихся на заданном расстоянии от центра. Это расстояние равно радиусу окружности.
Уравнение окружности с произвольным центром
Если центр окружности находится в точке (x0, y0), то уравнение окружности будет выглядеть так: (x - x0)^2 + (y - y0)^2 = R^2, где R - радиус окружности.
Уравнение окружности через заданную точку
Для составления уравнения окружности с центром в точке координат, проходящей через заданную точку (x0, y0), радиус окружности нужно вычислить. Радиус будет равен расстоянию от точки (x0, y0) до начала координат. Подставляя это значение в уравнение окружности, получаем: x^2 + y^2 = x0^2 + y0^2.
Построение окружности
Чтобы построить окружность по выведенным уравнениям, нужно разрешить их относительно y. Знак ± необходим, так как квадратный корень числа всегда неотрицателен. Чтобы построить окружность, удобнее составить её параметрическое уравнение, в котором обе координаты x и y зависят от параметра t.
Тригонометрическое представление окружности
Если окружность имеет единичный радиус с центром в начале координат, то точка (x, y) на этой окружности может быть представлена следующим образом: x = cos(t), y = sin(t), где t - угол, образованный отрезком, соединяющим центр окружности с точкой (x, y), и положительной полуосью x.
Обобщение уравнения окружности с произвольным центром
Формула x = R*cos(t) + x0, y = R*sin(t) + y0 может быть обобщена для окружности с произвольным центром (x0, y0) и радиусом R.