Что такое простое число
- Простые числа и их свойства
- Факторизация и разложение на простые множители
- Криптография и квантовые компьютеры
- Поиск и проверка простых чисел
- Бесконечность простых чисел
Простые числа и их свойства
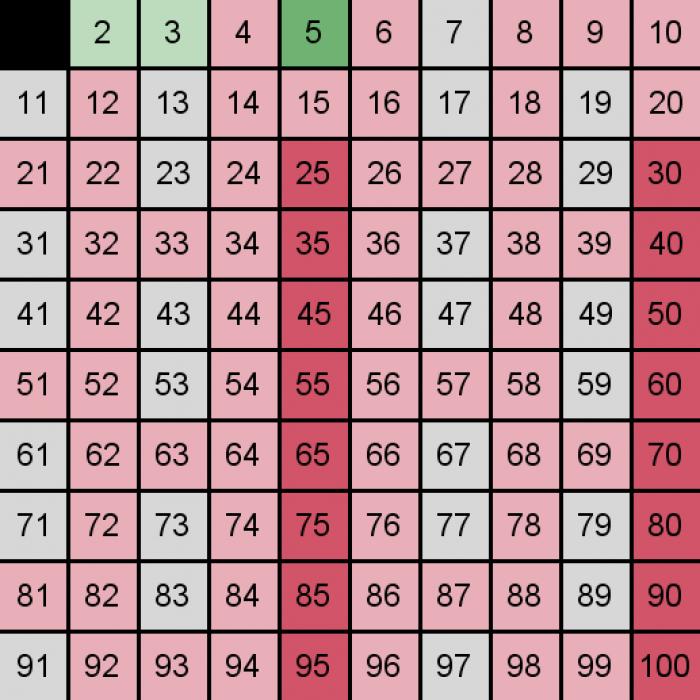
Простым числом называется натуральное число, которое делится только на единицу и само на себя. Все прочие числа, помимо единицы, являются составными. Свойства простых чисел изучает наука под названием теория чисел.
Факторизация и разложение на простые множители
Согласно основной теореме арифметики, любое натуральное число, которое больше единицы, может быть разложено на произведение простых чисел. Исходя из этого, можно сделать вывод о том, что простые числа представляют собой определенные "блоки" для натуральных чисел.
Операцию представления натурального числа в виде произведения простых называют факторизацией или разложением на простые множители. Полиномиальные алгоритмы разложения чисел неизвестны, но также нет доказательств того, что в природе они не существуют.
Криптография и квантовые компьютеры
На сложности вычислений, связанных с факторизацией чисел, основаны некоторые криптосистемы, например, одной из известных является RSA. Для квантовых компьютеров существует алгоритм Шора, который позволяет осуществлять факторизацию чисел с полиномиальной сложностью.
Поиск и проверка простых чисел
Существуют алгоритмы, с помощью которых можно осуществлять поиск, а также распознавать простые числа. Самыми простыми из них являются решето Эратосфена, решето Аткина, решето Сундарама. На деле же часто встает задача не получения простых чисел, а проверки числа на то, является ли оно простым. Алгоритмы, призванные решать подобные задачи, именуются тестами простоты.
Бесконечность простых чисел
Еще Евклидом был доказан тот факт, что простых чисел существует бесконечно много. Суть его доказательства, представленного в книге "Начала", заключается в следующем. Пусть существует конечное число простых чисел. Перемножим их, после чего прибавим к ним единицу. Число, которое получилось, не может быть разделено ни на какое простое число из конечного набора без остатка (он будет равен 1). В таком случае это число делится на простое число, которое не входит в состав представленного конечного набора. Помимо этого, существуют также и другие математические доказательства бесконечности простых чисел.