Как доказать, что отрезок - это биссектриса

- Доказательство равенства отрезка и биссектрисы
- Знание составляющих теоремы
- Понятие отрезка
- Доказательство теоремы
Доказательство равенства отрезка и биссектрисы
Задачи, связанные с поиском доказательства теорем в геометрии, являются распространенными. Одной из таких задач является доказательство равенства отрезка и биссектрисы.
Знание составляющих теоремы
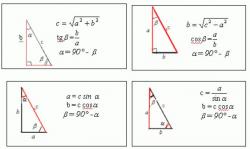
Для доказательства теоремы необходимо иметь представление о ее составляющих и их свойствах. Важно отметить, что биссектриса угла - это луч, выходящий из вершины угла и делящий его на два равных угла. Биссектриса угла также является особым геометрическим местом расположения точек внутри угла, которые равноудалены от его сторон. Согласно выдвигаемой теореме, биссектриса угла представляет собой отрезок, выходящий из угла и пересекающийся с противоположной стороной треугольника. Это утверждение следует доказать.
Понятие отрезка
Отрезок - это часть прямой, ограниченная двумя или более точками. В геометрии точка является абстрактным объектом без каких-либо характеристик, поэтому отрезок можно определить как расстояние между двумя точками, например, точками A и B. Точки, ограничивающие отрезок, называются его концами, а расстояние между ними - его длиной.
Доказательство теоремы
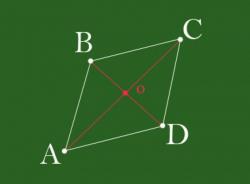
Для доказательства теоремы сформулируем ее подробное условие. Рассмотрим треугольник АВС с биссектрисой BK, выходящей из угла В. Необходимо доказать, что BK является отрезком.
Проведем через вершину С прямую СМ, которая будет параллельна биссектрисе ВК и пересекаться со стороной АВ в точке М. Для этого необходимо продолжить сторону треугольника.
Учитывая, что ВК является биссектрисой угла АВС, углы АВК и КВС равны между собой. Углы АВК и ВМС также равны, так как они являются соответственными углами двух параллельных прямых.
Также углы КВС и ВСМ равны, так как они лежат накрест при параллельных прямых. Следовательно, угол ВСМ равен углу ВМС, и треугольник ВМС является равнобедренным, значит, ВС=ВМ.
Используя теорему о параллельных прямых, пересекающих стороны угла, получим равенство: АК/КС=АВ/ВМ=АВ/ВС. Таким образом, биссектриса внутреннего угла делит противоположную сторону треугольника на пропорциональные его прилежащим сторонам части и является отрезком, что и требовалось доказать.