Как находить область определения
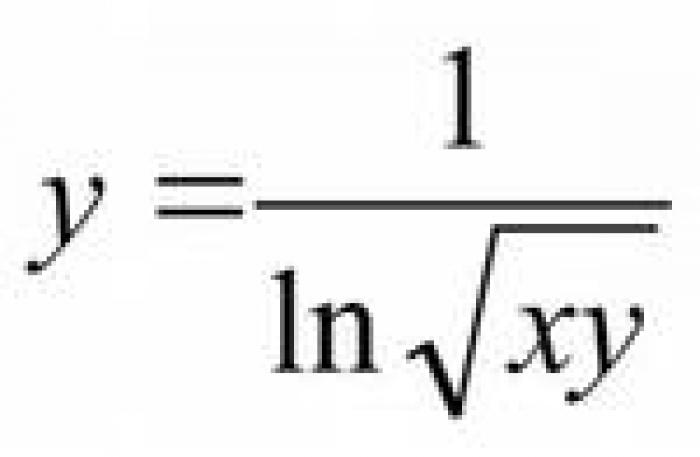
- Функция и ее область определения
- Как найти область определения функции?
- Область определения функции с дробью
- Область определения функции с корнем
- Область определения функции с логарифмом
- Область определения функции с обратными тригонометрическими функциями
- Область определения функции с несколькими видами исключений
Функция и ее область определения
Функция - это соответствие между числами, где каждому числу x из заданного множества сопоставляется единственное число y. Область определения функции - это множество всех допустимых значений аргумента x, при которых функция y=f(x) определена.
Как найти область определения функции?
Для различных видов функций существуют разные правила для определения исключений из области определения.
Область определения функции с дробью
Если функция содержит дробь, где знаменатель содержит переменную x, то знаменатель не должен быть равен нулю, иначе дробь не может существовать. Для определения области определения дроби, необходимо приравнять знаменатель к нулю и решить полученное уравнение. Найденные значения переменной x, которые делают знаменатель равным нулю, должны быть исключены из области определения функции.
Область определения функции с корнем
Если функция содержит корень четной степени, то подкоренное выражение должно быть положительным числом. Для определения области определения функции с корнем, необходимо решить неравенство, в котором подкоренное выражение меньше нуля. Значения переменной x, которые делают подкоренное выражение отрицательным, должны быть исключены из области определения функции.
Область определения функции с логарифмом
Для функций, содержащих логарифм, область определения состоит из всех чисел, которые больше нуля. Чтобы найти значения переменной x, не входящие в область определения, необходимо составить и решить неравенство, в котором выражение под логарифмом меньше нуля.
Область определения функции с обратными тригонометрическими функциями
Если функция содержит обратные тригонометрические функции, такие как арксинус и арккосинус, то они определены только на промежутке [-1;1]. Для определения области определения функции с обратными тригонометрическими функциями, необходимо проверить, при каких значениях переменной x выражение, стоящее под этими функциями, попадает в указанный промежуток.
Область определения функции с несколькими видами исключений
В некоторых функциях могут присутствовать сразу несколько видов исключений из области определения. В таком случае необходимо рассмотреть все возможные варианты и объединить результаты, чтобы получить область определения функции.
