Как найти диагонали призмы

- Призма и её диагональ
- Инструкция по нахождению диагонали призмы
- Виды призм и их классификация
- Вычисление диагонали призмы
- Вычисление диагонали призмы с помощью тригонометрических функций
- Пример вычисления диагонали призмы
Призма и её диагональ
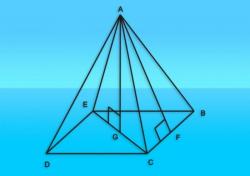
Призмой называется многогранная геометрическая фигура, основаниями которой являются конгруэнтные параллельные многоугольники, а боковыми гранями — параллелограммы. Нахождение диагонали призмы — одной из самых распространенных геометрических фигур в оптике - пример того, насколько взаимосвязаны основные положения геометрии.
Инструкция по нахождению диагонали призмы
Для вычисления диагонали призмы нам понадобятся несколько инструментов: калькулятор с тригонометрическими функциями, рулетка и угломер.
Виды призм и их классификация
Призмы бывают прямыми (боковые грани образуют прямой угол с основаниями) и наклонными. Прямые призмы делятся на правильные (их основаниями являются выпуклые многоугольники с равными сторонами и углами) и полуправильные (их грани — правильные многоугольники нескольких типов).
Вычисление диагонали призмы
Диагональю призмы называется отрезок, соединяющий вершины двух различных граней. Поскольку, исходя из определения призмы, ее диагональю является гипотенуза треугольника, задача по нахождению диагонали призмы сводится к вычислению одной из сторон этого треугольника по теореме Пифагора. Вариантов решения, в зависимости от исходных данных может быть несколько.
Вычисление диагонали призмы с помощью тригонометрических функций
Если известны величины углов, которые образует диагональ призмы с боковыми гранями или основанием, или же угол наклона граней призмы - катеты треугольника вычисляются с помощью тригонометрических функций. Само собой, только величины углов недостаточно — обычно в задачах дополнительно приводятся данные, необходимые для вычисления размера одного из катетов треугольника, гипотенуза которого является диагональю призмы.
Пример вычисления диагонали призмы
Допустим, нужно найти диагональ правильной четырехугольной призмы, если известны площадь ее основания и высота. Сначала определяем размер стороны основания, вычисляя квадратный корень из площади основания (квадрат - равносторонний прямоугольник). Затем вычисляем диагональ основания, которая равна стороне основания, умноженной на квадратный корень из двух. Гипотенуза призмы будет равна квадратному корню из суммы квадратов катетов, одним из которых является высота призмы (сторона боковой грани), а вторым — диагональ основания.
Таким образом, вычисление диагонали призмы требует применения различных геометрических методов и формул, в зависимости от заданных исходных данных. Это является важным элементом в оптике и других областях, где применяются призмы.