Как найти длину биссектрисы
- Понятие биссектрисы в геометрии
- Определения биссектрисы
- Свойства биссектрисы
- Биссектриса в равнобедренном треугольнике
- Формулы для нахождения биссектрисы произвольного треугольника
Понятие биссектрисы в геометрии
В курсе геометрии седьмого класса вводится понятие биссектрисы, которая является одной из трех основных линий треугольника и выражается через его стороны.
Определения биссектрисы
Существует несколько определений биссектрисы. Классические определения гласят, что биссектриса угла - это луч, выходящий из вершины угла и делящий его пополам, а биссектриса треугольника - это отрезок, соединяющий один из углов треугольника с противолежащей стороной и делящий данный угол пополам. Также можно использовать мнемоническое правило, которое гласит, что биссектриса - это крыса, бегающая по углам и делящая их пополам.
Свойства биссектрисы
Для полного представления о биссектрисе следует рассмотреть ее свойства. В любом треугольнике можно провести 3 биссектрисы, которые пересекаются в одной точке, являющейся центром вписанной окружности в данный треугольник. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. Биссектриса также является геометрическим местом точек, равноудаленных от сторон угла.
Биссектриса в равнобедренном треугольнике
В равнобедренном треугольнике биссектриса, проведенная к основанию, является одновременно медианой и высотой. Для нахождения биссектрисы в таком треугольнике используется теорема Пифагора.
Формулы для нахождения биссектрисы произвольного треугольника
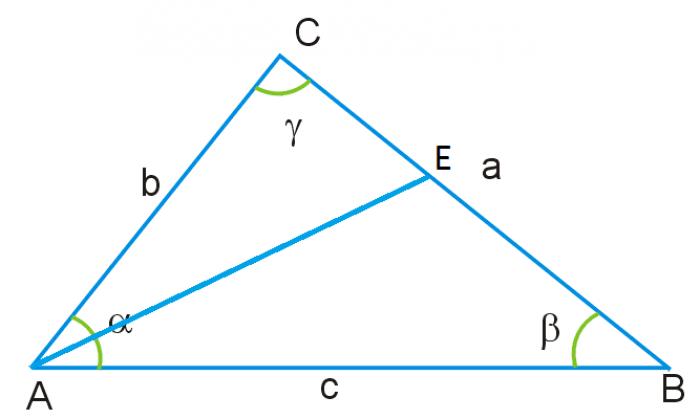
Формулы для нахождения биссектрисы произвольного треугольника выводятся из теоремы Стюарта, которую сформулировал английский математик М. Стюарт. Если обозначить стороны треугольника буквами a, b, c, где AB = c, BC = a, AC = b, то длина биссектрисы, опущенной на сторону b из угла ABC, обозначается как Lc. Биссектриса делит сторону b на отрезки al и cl, а углы треугольника при вершинах A, B и C обозначаются соответственно. Также вводится высота треугольника H, проведенная из вершины B на сторону b.