Как найти длину диагоналей трапеции
- Трапеция: основные свойства и способы вычисления
- Определение оснований и высоты трапеции
- Вычисление высоты трапеции
- Вычисление других сторон трапеции
- Вычисление второй диагонали и полезный совет
Трапеция: основные свойства и способы вычисления
Трапеция - это выпуклый четырехугольник, у которого параллельны две противоположные стороны. Если и другие две параллельны, то это параллелограмм. Фигура называется трапецией, если другие две стороны непараллельны.
Определение оснований и высоты трапеции
Основаниями трапеции называются параллельные стороны, а две другие - боковые стороны. Расстояние между основаниями является высотой трапеции.
Вычисление высоты трапеции
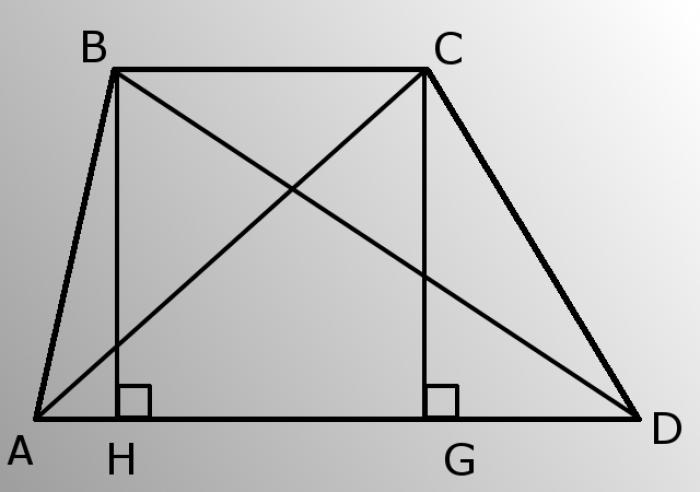
Для вычисления высоты трапеции нам понадобятся боковые стороны (AB и CD) и угол A (BAD). Проведем высоту BH и найдем ее длину из треугольника ABH. Треугольник ABH является прямоугольным, поэтому катет BH равен произведению гипотенузы AB на синус угла А. Таким образом, BH=AB*sinA.
Вычисление других сторон трапеции
Теперь мы можем вычислить AH по теореме Пифагора из прямоугольного треугольника ABH. Квадрат гипотенузы AB равен сумме квадратов катетов BH и AH. Таким образом, AH = корень(AB*AB-HB*HB).
Затем мы рассматриваем треугольник BDH и вычисляем сторону HD. HD равна разности AD и AH, то есть HD=AD-AH.
Из прямоугольного треугольника BDH мы можем вывести гипотенузу BD по той же теореме Пифагора. BD равна корню из суммы квадратов сторон BH и HD. Таким образом, вам известна одна из диагоналей трапеции.
Вычисление второй диагонали и полезный совет
Далее проведем высоту CG. Поскольку основания трапеции параллельны, высоты BH и CG равны.
Из прямоугольного треугольника CGD мы можем вычислить катет GD по теореме Пифагора. GD равен корню из разности квадрата стороны CD и квадрата стороны CG.
Теперь для треугольника ACG мы можем найти сторону AG, которая равна разности AD и GD.
Наконец, по теореме Пифагора, мы можем вычислить диагональ AC из прямоугольного треугольника ACG. AC равна корню из суммы квадратов сторон AG и CG.
В результате выполнения этих шагов мы получаем обе диагонали трапеции.
Полезный совет: если трапеция равнобедренная, то длины диагоналей равны, поэтому достаточно найти только одну из них.
