Как найти длину хорды, стянутой дугой
- Что такое хорда и дуга?
- Вычисление длины хорды на основе длины дуги и радиуса окружности
- Вычисление центрального угла
- Вычисление длины хорды
Что такое хорда и дуга?
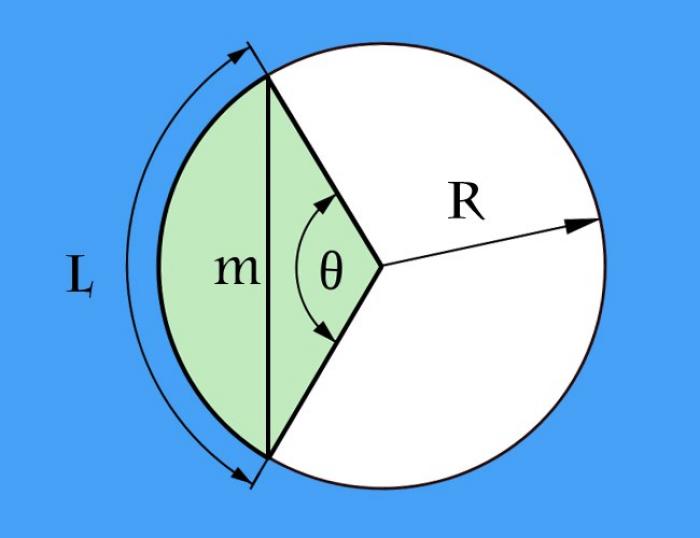
Хордой называется отрезок, соединяющий две произвольные точки на любой кривой линии. Дуга же представляет собой часть этой кривой, заключенную между крайними точками хорды. Понятия хорды и дуги применимы к любой форме кривой линии.
Вычисление длины хорды на основе длины дуги и радиуса окружности
Если известна длина дуги (l) между крайними точками, задающими хорду, а также радиус окружности (R), то можно рассчитать длину хорды (m) путем вычисления длины основания равнобедренного треугольника.
Вычисление центрального угла
Для вычисления длины хорды необходимо определить величину центрального угла. Разделите длину дуги на радиус (l/R), чтобы получить этот угол в радианах. Если предпочитаете работать с градусами, формула будет сложнее: умножьте длину дуги на 360 и разделите результат на удвоенное произведение числа Пи на радиус (l*360/(2*π*R) = l*180/(π*R)).
Вычисление длины хорды
После определения величины центрального угла, можно рассчитать длину хорды. Умножьте удвоенный радиус круга на синус половины центрального угла. Для расчетов в градусах формула будет выглядеть следующим образом: m = 2*R*sin(l*90/(π*R)). В случае вычислений в радианах формула будет проще: m = 2*R*sin(l/(2*R)).
Вычисление длины хорды при известной длине дуги и полной длине окружности
Если помимо длины дуги (l) также дана полная длина окружности (L), выразите радиус как L/(2*π). Подставьте это выражение в общую формулу из предыдущего шага: m = 2*(L/(2*π))*sin(l*90/(π*L/(2*π))). После упрощения у вас должно получиться равенство для расчетов в градусах: m = L/π*sin(l*180/L). В случае вычислений в радианах формула будет выглядеть следующим образом: m = L/π*sin(l*π/L).
Вычисление длины хорды может быть полезно при работе с кругами и окружностями. Эта информация поможет определить длину отрезка, соединяющего две точки на окружности и применима в различных областях, таких как геометрия, физика и инженерия.






