Как найти длину медианы
- Что такое медиана треугольника и как ее найти?
- Нахождение медианы в общем случае
- Медиана в равнобедренном треугольнике
- Медиана в равностороннем треугольнике
- Нахождение медианы по другим данным
Что такое медиана треугольника и как ее найти?
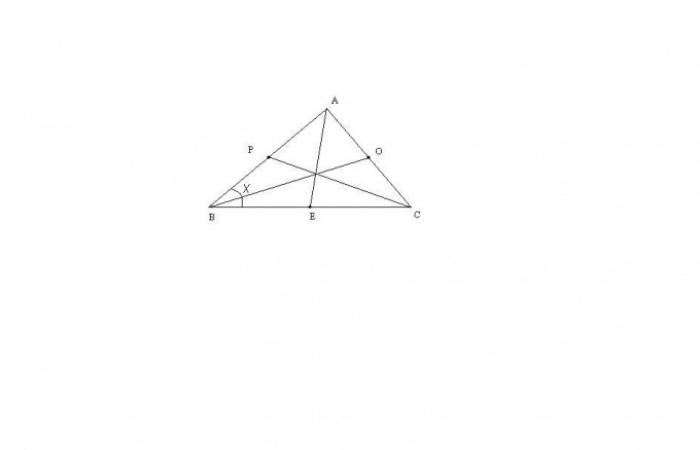
Медиана - это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны. Она играет важную роль в геометрии и может быть найдена с использованием различных данных о треугольнике.
Нахождение медианы в общем случае
Для треугольника ABC с тремя не равными сторонами можно найти длину медианы AE с помощью следующей формулы: AE = sqrt(2*(AB^2)+2*(AC^2)-(BC^2))/2. Таким же образом можно найти и другие медианы треугольника. Эта формула выводится через теорему Стюарта или через достроение треугольника до параллелограмма.
Медиана в равнобедренном треугольнике
Если треугольник ABC равнобедренный и AB = AC, то медиана AE будет одновременно являться высотой этого треугольника. Треугольник BEA будет прямоугольным, и его длина медианы может быть найдена с использованием теоремы Пифагора: АЕ = sqrt((AB^2)-(BC^2)/4). Для медиан BO и СP, справедливо следующее: BO = CP = sqrt(2*(BC^2)+(AB^2))/2.
Медиана в равностороннем треугольнике
В равностороннем треугольнике ABC все медианы равны друг другу. Угол при вершине такого треугольника равен 60 градусам, поэтому AE = BO = CP = a*sqrt(3)/2, где a - длина стороны равностороннего треугольника (AB = AC = BC).
Нахождение медианы по другим данным
Медиану треугольника также можно найти, используя другие данные. Например, если заданы длины двух сторон (AB и BC), к одной из которых проведена медиана, а также угол x между ними, то длину медианы можно найти с помощью теоремы косинусов: AE = sqrt((AB^2+(BC^2)/4)-AB*BC*cos(x)).
Медиана треугольника является важным понятием в геометрии и может быть найдена различными способами в зависимости от данных о треугольнике. Надеюсь, что эта статья помогла вам лучше понять его свойства и способы нахождения.






