Как найти длину медианы в треугольнике
- Медиана треугольника: определение и свойства
- Задача 1: нахождение длины медианы
- Решение задачи 1
- Задача 2: нахождение длины медианы в равнобедренном треугольнике
- Решение задачи 2
- Задача 3: нахождение длин трех медиан
- Решение задачи 3
Медиана треугольника: определение и свойства
Медиана треугольника - это отрезок, проведенный из любой его вершины к противоположной стороне, при этом он делит ее на части равной длины. Максимальное число медиан в треугольнике - три, по количеству вершин и сторон.
Задача 1: нахождение длины медианы
Дан произвольный треугольник ABD, в котором проведена медиана BE. Требуется найти длину медианы BE, если известны длины сторон AB = 10 см, BD = 5 см и AD = 8 см.
Решение задачи 1
Для нахождения длины медианы BE применим формулу медианы, выраженную через все стороны треугольника: BE = √((2*AB^2 + 2*BD^2 - AD^2)/4) = √((200 + 50 - 64)/4) = √(46,5) ≈ 6,8 см.
Задача 2: нахождение длины медианы в равнобедренном треугольнике
Дан равнобедренный треугольник ABD, в котором стороны AD и BD равны. Из вершины D проведена медиана на сторону BA, которая составляет угол 90° с BA. Требуется найти длину медианы DH, если известны длина стороны BA = 10 см и угол DBA = 60°.
Решение задачи 2
Для нахождения длины медианы DH определим одну из равных сторон треугольника AD или BD. Рассмотрим прямоугольный треугольник BDH. Из определения медианы следует, что BH = BA/2 = 10/2 = 5. Найдем сторону BD по тригонометрической формуле из свойства прямоугольного треугольника: BD = BH/sin(DBH) = 5/sin60° = 5/(√3/2) ≈ 5,8. Теперь возможны два варианта нахождения длины медианы DH: по формуле, использованной в первой задаче или по теореме Пифагора для прямоугольного треугольника BDH: DH^2 = BD^2 - BH^2. Получаем DH^2 ≈ 8,6 см.
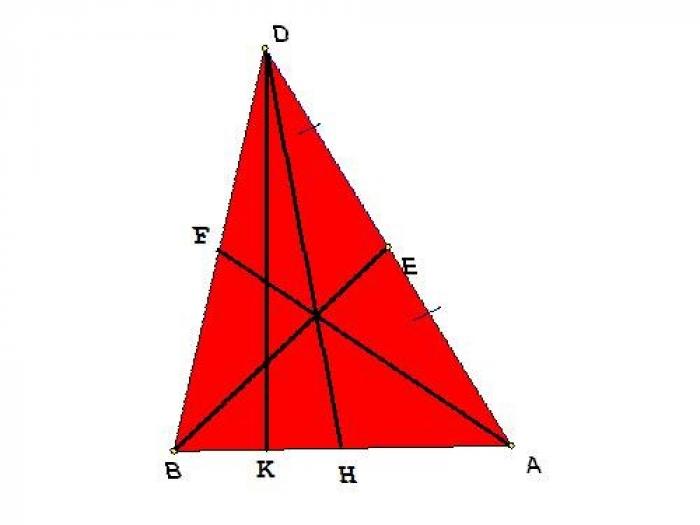
Задача 3: нахождение длин трех медиан
Дан произвольный треугольник BDA, в котором проведены три медианы. Требуется найти длины всех трех медиан, если известно, что высота DK равна 4 см и делит основание на отрезки длиной BK = 3 см и KA = 6 см.
Решение задачи 3
Для нахождения длин медиан необходимы длины всех сторон треугольника. Длину BA можно найти из условия: BA = BH + HA = 3 + 6 = 9. Рассмотрим прямоугольный треугольник BDK. По теореме Пифагора найдем длину гипотенузы BD: BD^2 = BK^2 + DK^2; BD = √(9 + 16) = √25 = 5. Аналогично найдем гипотенузу прямоугольного треугольника KDA: AD^2 = DK^2 + KA^2; AD = √(16 + 36) = √52 ≈ 7,2. По формуле выражения через стороны найдем медианы:
BE^2 = (2*BD^2 + 2*BA^2 - AD^2)/4 = (50 + 162 - 51,8)/4 ≈ 40, отсюда BE ≈ 6,3 см.
DH^2 = (2*BD^2 + 2*AD^2 - BA^2)/4 = (50 + 103,7 - 81)/4 ≈ 18,2, отсюда DH ≈ 4,3 см.
AF^2 = (2*AD^2 + 2*BA^2 - BD^2)/4 = (103,7 + 162 - 25)/4 ≈ 60, отсюда AF ≈ 7,8 см.
