Как найти длину перпендикуляра

Содержание:

1. Что такое перпендикуляр?
2. Как рассчитать длину перпендикуляра на плоскости?
3. Шаг 1: Подстановка координат точки в уравнение прямой
4. Шаг 2: Рассчет нормирующего множителя
5. Шаг 3: Приведение уравнения прямой к нормальному виду
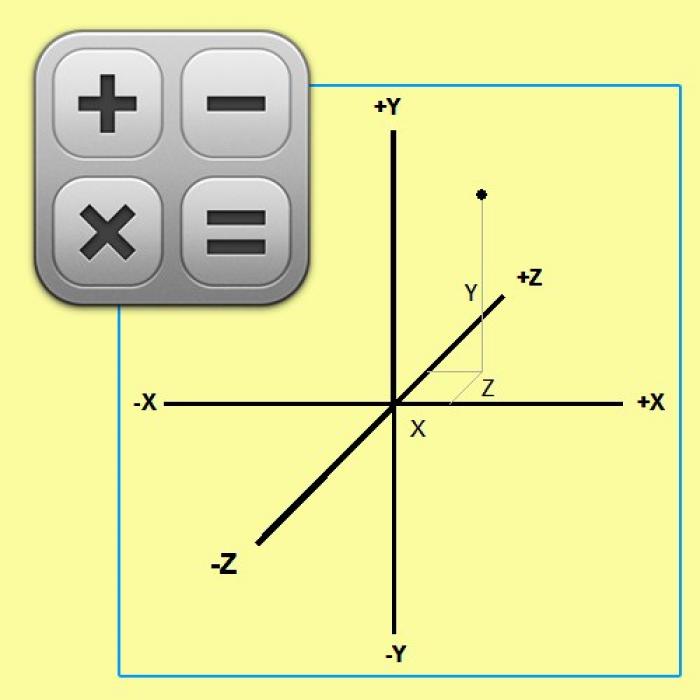
6. Как рассчитать длину перпендикуляра в трехмерном пространстве?

Что такое перпендикуляр?

Перпендикуляр - это прямая, которая пересекает заданную линию под углом в 90°. Однако, так как прямая является бесконечной, говорить о длине перпендикуляра неправильно. Обычно под длиной перпендикуляра понимают расстояние между двумя точками, лежащими на этой перпендикуляре. Например, это может быть расстояние между заданной точкой и ее нормальной проекцией на плоскость или между точкой в пространстве и точкой пересечения перпендикуляра, опущенного из нее, с прямой линией.

Как рассчитать длину перпендикуляра на плоскости?

Если необходимо рассчитать длину перпендикуляра, опущенного из точки A(X₁;Y₁) на прямую, заданную уравнением a*X + b*Y + C = 0, следуйте следующей инструкции:

Шаг 1: Подстановка координат точки в уравнение прямой

Сначала подставьте координаты точки A(X₁;Y₁) в уравнение прямой и рассчитайте абсолютное значение левой части тождества: |a*X₁ + b*Y₁ + C|. Например, при координатах точки A(15;-17) и уравнении прямой 3*X + 4*Y + 140 = 0 результатом этого шага будет число |3*15 + 4*(-17) + 140| = |45-61+140| = 124.

Шаг 2: Рассчет нормирующего множителя

Рассчитайте нормирующий множитель, который является дробью, в числителе которой стоит единица, а в знаменателе - квадратный корень из суммы квадратов множителей по обеим координатным осям из уравнения прямой: 1/√(X²+Y²). Для примера, рассмотренного выше, величина нормирующего множителя будет равна 1/√(3²+4²) = 1/√25 = 0,2.

Шаг 3: Приведение уравнения прямой к нормальному виду

Приведите уравнение прямой к нормальному виду, умножив обе части равенства на нормирующий множитель. В общем виде результат должен быть представлен уравнением: (a*X+b*Y+C)/√(X²+Y²) = 0. Левая часть этого уравнения определяет длину перпендикуляра в общем виде: d = (a*X+b*Y+C)/√(X²+Y²). В практических расчетах просто перемножьте число, полученное на первом шаге, и рассчитанный на втором шаге коэффициент. Для примера, рассмотренного на первом шаге, ответом будет число 124*0,2=24,8 - такова длина перпендикулярной линии отрезка, соединяющей заданную точку с перпендикуляром.

Как рассчитать длину перпендикуляра в трехмерном пространстве?

Для нахождения длины перпендикуляра, опущенного из точки A(X₁;Y₁;Z₁) на плоскость, заданную уравнением a*X + b*Y + c*Z + D = 0, используйте такую же последовательность операций. В этом случае, под знак радикала в нормирующем множителе добавится третье слагаемое √(X²+Y²+Z²), как и в числителе дроби формулы, определяющей длину перпендикуляра в общем виде: d = (a*X+b*Y+c*Z+D)/√(X²+Y²+Z²).

Таким образом, с помощью этих шагов вы сможете рассчитать длину перпендикуляра на плоскости или в трехмерном пространстве.