Как найти гипотенузу при известном катете
- Что такое катеты и гипотенуза в прямоугольном треугольнике?
- Как найти длину гипотенузы с использованием теоремы Пифагора?
- Формула Пифагора для нахождения длины гипотенузы
- Пример применения теоремы Пифагора
Что такое катеты и гипотенуза в прямоугольном треугольнике?
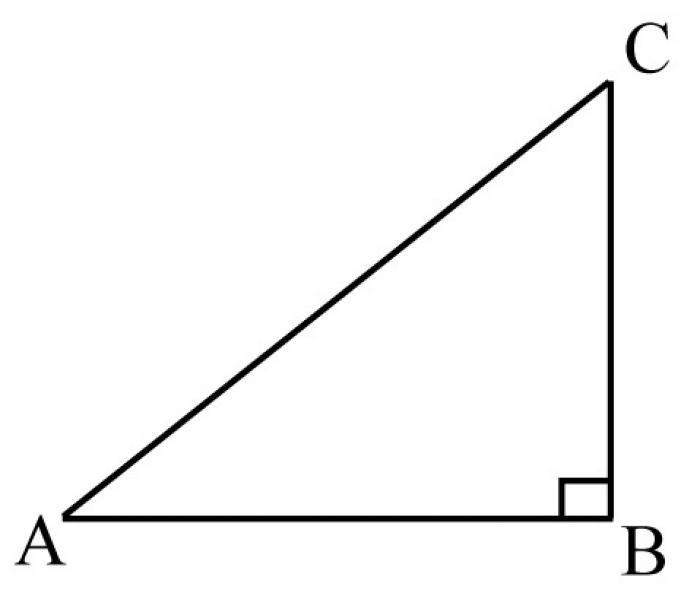
В прямоугольном треугольнике есть три стороны: две катеты и гипотенуза. Катеты - это стороны, которые образуют прямой угол, а гипотенуза - самая длинная сторона, которая противоположна прямому углу.
Как найти длину гипотенузы с использованием теоремы Пифагора?
Для того чтобы найти длину гипотенузы, необходимо знать длины катетов и использовать теорему Пифагора. Эта теорема утверждает, что квадрат длины гипотенузы равен сумме квадратов длин катетов.
Формула Пифагора для нахождения длины гипотенузы
Формула Пифагора выглядит следующим образом: c² = a² + b², где c - длина гипотенузы, a и b - длины катетов.
Пример применения теоремы Пифагора
Давайте рассмотрим пример. Пусть длина одного из катетов равна 3 см, а длина другого катета равна 4 см. Тогда сумма их квадратов будет равна 25 см²: 9 см² + 16 см² = 25 см². Используя формулу Пифагора, мы можем найти длину гипотенузы: c = √(a² + b²). В данном случае, это будет равно квадратному корню из 25 см², то есть 5 см.
Таким образом, длина гипотенузы прямоугольного треугольника с катетами длиной 3 см и 4 см равна 5 см.






