Как найти касательное уравнение

- Касательная к графику: определение и составление уравнения
- Инструкция для составления уравнения касательной
- Пример использования алгоритма
- 1. Обозначим х буквой а, т.е. а=1.
- 2. Вычислим f(a). В данном случае f(a) = 1/(1) = 1.
- Полезный совет
Касательная к графику: определение и составление уравнения
В учебнике 11 класса по алгебре учащиеся изучают тему производных, в которой особое внимание уделяется касательной к графику и способу нахождения ее уравнения. В этой статье мы рассмотрим инструкцию для составления уравнения касательной, а также решим пример для лучшего понимания данного алгоритма.
Инструкция для составления уравнения касательной
Итак, пускай у нас есть функция y=f(x) и определенная точка М с координатами а и f(a). Предположим, что существует производная f'(a). Для составления уравнения касательной нам необходимо найти значения неизвестных k и m. Как известно, уравнение касательной имеет вид y=kx+m, поэтому для нахождения k и m мы используем следующие шаги:
1. Найдите угловой коэффициент k. Если точка М принадлежит графику и от нее можно провести касательную, не перпендикулярную к оси абсцисс, то k равен f'(a).
2. Вычислите значение m, используя тот факт, что искомая прямая проходит через точку М. Подставьте координаты точки М в уравнение прямой: f(a)=ka+m. Отсюда можно найти m, выразив его как m=f(a)-ka.
3. Подставьте найденные значения коэффициентов в уравнение прямой: y=f(a)+f'(a)(x-a). Таким образом, уравнение касательной имеет вид y=f(a)+f'(a)(x-a).
Пример использования алгоритма
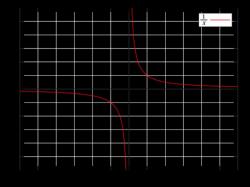
Для лучшего понимания алгоритма рассмотрим следующую задачу: составить уравнение касательной для функции y=1/x в точке х=1.
1. Обозначим х буквой а, т.е. а=1.
2. Вычислим f(a). В данном случае f(a) = 1/(1) = 1.
3. Найдем производную от х, f'(x). В нашем примере f'(x) = -1/(x^2). Теперь вычислим f'(a), подставив вместо х значение а: f'(a) = -1/(1^2) = -1.
4. Подставим найденные числа в уравнение касательной: y=f(a)+f'(a)(x-a). Получаем y=1+(-1)(x-1) = 1-x.
Таким образом, уравнение касательной к графику функции y=1/x в точке х=1 имеет вид y=1-x.
Полезный совет
Для подтверждения найденного уравнения касательной вы можете построить график функции и полученной прямой. Это поможет визуально убедиться в правильности решения задачи.