Как найти корень квадрата
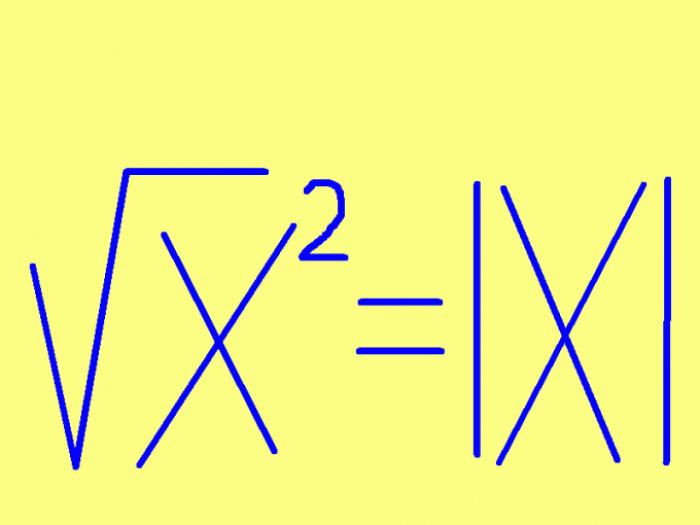
- Корень квадратный из квадрата: правила и упрощение выражений
- Правила нахождения корня квадратного числа
- Нахождение корня квадратного числового выражения
- Нахождение корня из квадрата выражения с параметром
- Удобные формулы при нахождении корня квадратного из квадрата
Корень квадратный из квадрата: правила и упрощение выражений
В математических задачах иногда возникает выражение "корень квадратный из квадрата". Некоторые люди склонны сокращать эту конструкцию, отбрасывая знак корня и квадрата, так как эти операции являются взаимно обратными. Однако такое упрощение не всегда является корректным и может привести к неверным результатам.
Правила нахождения корня квадратного числа
Чтобы найти корень квадратный числа, необходимо учесть его знак. Если число неотрицательное (положительное или ноль), то корень квадратный будет равен самому числу. Если возводимое в квадрат число отрицательное, то корень квадратный из его квадрата будет равен противоположному числу, умноженному на -1. Иными словами, корень квадратный числа равен этому числу без знака. Можно записать это правило формулой: корень квадратный из x² = |x|, где |x| - модуль (абсолютное значение) числа x. Например: √10² = 10, √0² = 0, √(-5)² = 5.
Нахождение корня квадратного числового выражения
Чтобы найти корень квадратный числового выражения, сначала нужно вычислить значение этого выражения. Затем, в зависимости от знака получившегося числа, действовать согласно описанным ранее правилам. Например: √(2-5)² = √(-3)² = 3.
Если требуется продемонстрировать порядок действий, то можно вернуть исходную форму выражения после извлечения корня. Например: √(2-5)² = √(-3)² = 3 = -(2-5), или √(2-5)² = √(-3)² = 3 = 5-2.
Нахождение корня из квадрата выражения с параметром
Для нахождения корня из квадрата выражения с параметром (переменным числовым значением), необходимо определить области положительных и отрицательных значений выражения. Для этого нужно определить соответствующие значения параметра. Например, если нужно упростить выражение √(п-100)², где п - параметр, найдите значения параметра, при которых выражение положительно и отрицательно. В данном случае, при п<100, выражение отрицательно. Следовательно, √(п-100)² = п-100 при п ≥100 и √(п-100)² = 100-п при п<100.
Удобные формулы при нахождении корня квадратного из квадрата
Классическая форма ответа для задач нахождения корня из квадрата может быть громоздкой и не очень удобной на практике. Поэтому в программе Excel можно оставить выражение в исходном виде, используя формулу: =КОРЕНЬ(СТЕПЕНЬ((B1-100),2)), или преобразовать его к более простой формуле: =ABS(B1-100), где В1 - адрес клетки, содержащей значение параметра "п". Второй вариант предпочтительнее, так как позволяет получить более точные и быстрые вычисления.






