Как найти максимальное значение функции
- Исследование функции на максимум
- Определение определенности функции
- Исследование линейной функции
- Исследование функции на экстремумы
- Определение типа экстремума
- Использование второй производной
- Выбор максимального значения
Исследование функции на максимум
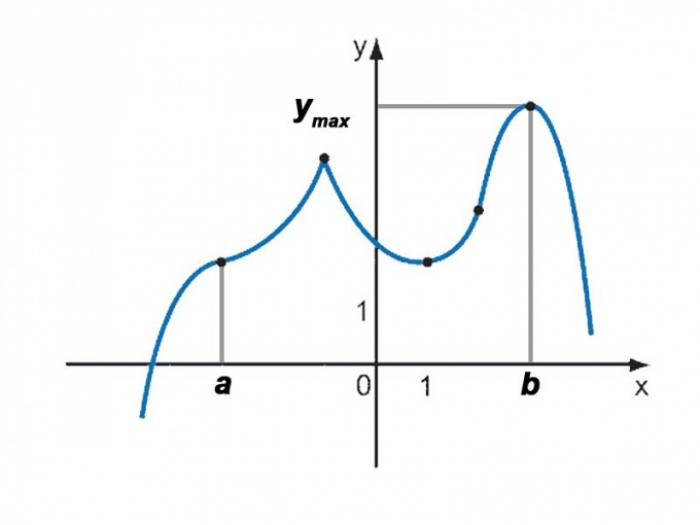
Пусть дана некоторая функция, заданная аналитически, то есть выражением вида f(x). Чтобы вычислить максимальное значение функции на заданном отрезке [a, b], необходимо провести исследование функции и определить точки экстремума.
Определение определенности функции
Прежде всего, нужно установить, определена ли заданная функция на всем отрезке [a, b]. Если у функции есть точки разрыва, то необходимо определить их тип. Например, функция f(x) = 1/x не имеет ни максимального, ни минимального значения на отрезке [-1, 1], так как в точке x = 0 функция стремится к плюс бесконечности справа и к минус бесконечности слева.
Исследование линейной функции
Если заданная функция является линейной, то есть задана уравнением вида y = kx + b, где k ≠ 0, то можно определить ее монотонность. Если k > 0, функция монотонно возрастает на всей своей области определения. Если k < 0, функция монотонно убывает на всей своей области определения.
Исследование функции на экстремумы
Даже если установлено, что значение функции на одном из концов отрезка больше, чем на другом, функция может достигать больших значений в точке максимума. Чтобы найти точку максимума, необходимо использовать производную функции. Если в точке x0 функция имеет экстремум (максимум, минимум или стационарную точку), то ее производная в этой точке обращается в ноль: f'(x0) = 0.
Определение типа экстремума
Для определения, какой из трех видов экстремума (максимум, минимум или стационарная точка) находится в обнаруженной точке, необходимо исследовать поведение производной в окрестностях этой точки. Если производная меняет знак с плюса на минус, то есть монотонно убывает, то функция имеет максимум в найденной точке. Если производная меняет знак с минуса на плюс, то есть монотонно возрастает, то функция имеет минимум в найденной точке. Если производная не меняет знака, то это стационарная точка для функции.
Использование второй производной
В случаях, когда вычислить знаки производной в окрестности найденной точки сложно, можно воспользоваться второй производной и определить знак этой функции в точке x0. Если вторая производная больше нуля, то найдена точка минимума. Если вторая производная меньше нуля, то найдена точка максимума.
Выбор максимального значения
Для окончательного решения задачи необходимо выбрать максимальное из значений функции на концах отрезка и во всех найденных точках максимума. Это значение будет являться максимальным значением функции на заданном отрезке [a, b].
