Как найти модуль вектора перемещения

- Математические методы в кинематике
- Модуль вектора перемещения
- Путь и расстояние
- Вычисление модуля вектора перемещения
- Формула для вычисления модуля вектора перемещения
- Важное свойство перемещения
Математические методы в кинематике
В кинематике, науке, изучающей движение тел в пространстве, широко используются математические методы для нахождения различных величин. Один из таких методов - векторная алгебра, которая позволяет найти модуль вектора перемещения.
Модуль вектора перемещения
Для нахождения модуля вектора перемещения необходимо знать координаты точек начала и конца вектора, то есть первоначального и итогового положения тела. Это позволяет применить формулу из векторной алгебры.
Путь и расстояние
Во время движения материальное тело изменяет свое положение в пространстве. Длина его траектории составляет путь тела, но не расстояние, на которое оно переместилось. Несмотря на то, что эти две величины совпадают только в случае прямолинейного движения, векторная алгебра все равно позволяет найти модуль вектора перемещения для любой траектории.
Вычисление модуля вектора перемещения
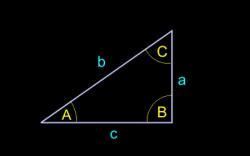
Для вычисления модуля вектора перемещения необходимо провести отрезок из точки начального положения тела в точку конечного положения. Затем необходимо опустить проекции его концов на оси и нарисовать параллельные и равные им отрезки, проходящие через рассматриваемые точки. Полученный рисунок образует прямоугольный треугольник с катетами-проекциями и гипотенузой-перемещением.
С использованием теоремы Пифагора можно найти длину гипотенузы, которая и будет модулем вектора перемещения. Для этого необходимо запиcать длины катетов, которые равны разностям между соответствующими координатами точек начального и конечного положения тела.
Формула для вычисления модуля вектора перемещения
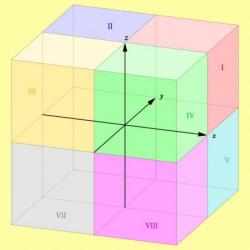
Для двумерного пространства формула вычисления модуля вектора перемещения выглядит следующим образом: |AB| = √(ABx² + ABy²) = √((x – x0)² + (y – y0)²). Если рассматривается трехмерное пространство, в формулу добавляется третья координата, аппликата z: |AB| = √(ABx² + ABy² + ABz²) = √((x – x0)² + (y – y0)² + (z – z0)²).
Важное свойство перемещения
Модуль вектора перемещения обладает важным свойством - он всегда меньше или равен длине пути. В общем случае линия перемещения не совпадает с кривой траекторией. Проекции вектора перемещения могут быть как больше, так и меньше нуля, однако в расчете они участвуют в четной степени, поэтому их значения не имеют значения.