Как найти объем параллелепипеда
- Что такое параллелепипед и его определение в геометрии
- Различные определения параллелепипеда
- Специфические виды параллелепипеда
- Определение объема параллелепипеда
- Альтернативный метод определения объема параллелепипеда
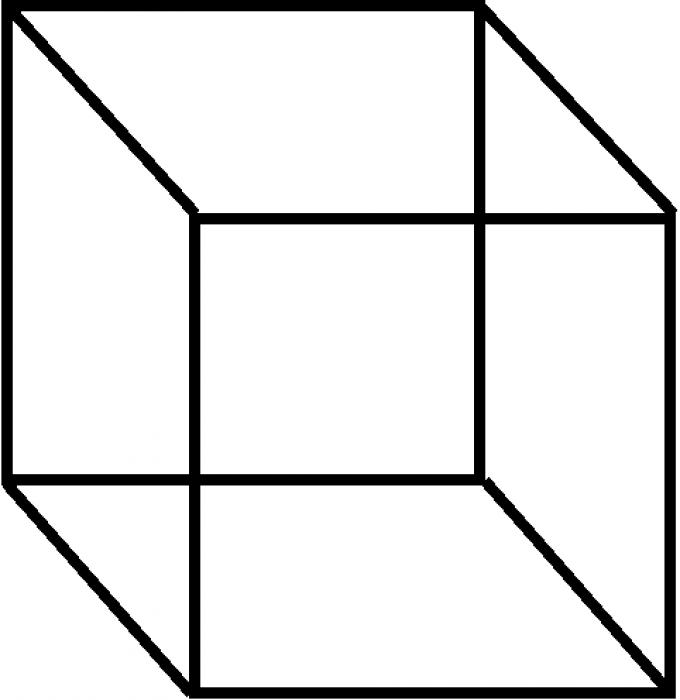
Что такое параллелепипед и его определение в геометрии
В геометрии параллелепипед представляет собой трехмерную фигуру, состоящую из шести параллелограммов. Термин "ромбоид" также иногда используется для обозначения параллелепипеда.
В Евклидовой геометрии существуют четыре понятия, которые определяют параллелепипед: параллелограмм, параллелепипед, куб и квадрат. В данном контексте геометрии, где углы не дифференцируются, определение параллелепипеда допускает только параллелограмм и параллелепипед.
Различные определения параллелепипеда
Существуют три эквивалентных определения параллелепипеда:
1. Параллелепипед - это многогранник с шестью гранями, каждая из которых является параллелограммом.
2. Параллелепипед - это шестигранник с тремя парами параллельных граней.
3. Параллелепипед - это призма, у которой основой служит параллелограмм.
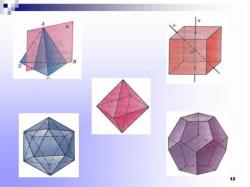
Специфические виды параллелепипеда
Существуют несколько конкретных видов параллелепипеда:
1. Прямоугольный кубоид состоит из шести прямоугольных граней.
2. Куб состоит из шести квадратных сторон.
3. Шестисторонний ромб - это еще один вид параллелепипеда.
Определение объема параллелепипеда
Объем параллелепипеда определяется как произведение площади его основы (A) на его высоту (H). Основа - это одна из шести граней параллелепипеда, а высота - перпендикулярное расстояние между основой и противоположной стороной.
Альтернативный метод определения объема параллелепипеда
Существует альтернативный метод определения объема параллелепипеда, который использует его векторы. Пусть вектор a = (A1, A2, A3) и вектор b = (B1, B2, B3). Тогда объем параллелепипеда равен абсолютной величине тройного скалярного произведения a • (b × c): A = |b| |c| sin(θ), где θ - угол между векторами b и c, а высота h = |a| sin(α), где α - внутренний угол между векторами a и h.
В заключение, параллелепипед - это многогранная фигура, образованная шестью параллелограммами. Он имеет несколько определений и специфических видов, а его объем можно определить как произведение площади основы на высоту. Существует также альтернативный метод определения объема параллелепипеда, использующий векторы.