Как найти область сходимости ряда
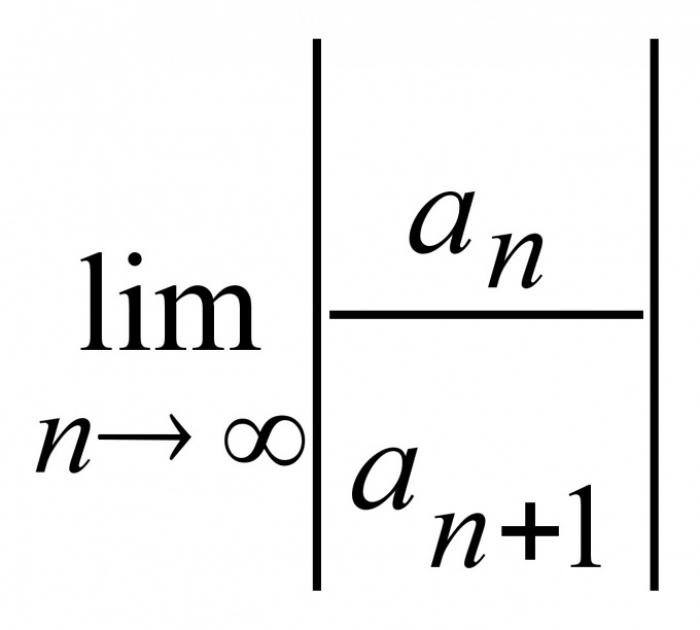
- Изучение сходимости числовых рядов
- Проверка сходимости ряда
- Сравнение рядов
- Оценка сходимости ряда
- Знакочередующиеся ряды
- Степенные ряды
- Пример разложения в ряд Маклорена
Изучение сходимости числовых рядов
Исследование функций часто становится проще, когда они разложены в числовой ряд. Однако, для анализа таких рядов необходимо уметь определять и анализировать их сходимость.
Проверка сходимости ряда
Для определения сходимости заданного ряда, необходимо сначала проверить, стремится ли его общий член к нулю при бесконечном возрастании n. Если предел общего члена не равен нулю, то ряд расходится. Если же предел равен нулю, то ряд, возможно, сходящийся.
Сравнение рядов
Если заданы два ряда, общие члены которых соответственно равны Un и Vn, то их можно сравнивать, если существует такое конечное N, начиная с которого Un ≥ Vn. Если известно, что ряд U сходится, то ряд V также сходится, а если ряд V расходится, то и ряд U также расходится.
Оценка сходимости ряда
Если все члены ряда положительны, то его сходимость можно оценивать по признаку Даламбера. Найдите коэффициент p = lim(U(n+1)/Un) при n → ∞. Если p < 1, то ряд сходится. При p > 1 ряд расходится, а если p = 1, то требуется дополнительное исследование.
Знакочередующиеся ряды
Если знаки членов ряда чередуются, то такой ряд называется знакопеременным или знакочередующимся. Сходимость такого ряда определяется признаком Лейбница. Если общий член при возрастании n стремится к нулю, и каждый следующий член меньше предыдущего, то ряд сходится.
Степенные ряды
При анализе функций часто используются степенные ряды. Сходимость такого ряда зависит от значения x. Радиус сходимости, обозначаемый как R, определяет диапазон значений x, при которых ряд сходится. Для анализа сходимости ряда необходимо найти R и проверить его на границе диапазона.
Пример разложения в ряд Маклорена
Например, ряд разложения функции e^x в ряд Маклорена имеет следующий вид: e^x = 1 + x + (x^2)/2! + (x^3)/3! + ... + (x^n)/n! + ...
При анализе этого ряда, отношение an/a(n+1) равно (1/n!)/(1/(n+1)!) = (n+1)!/n! = n + 1. Предел этого отношения при n → ∞ равен ∞. Следовательно, R = ∞, и ряд сходится на всей действительной оси.
Исследование и анализ числовых рядов является важной задачей при изучении функций. Правильное определение сходимости ряда позволяет более эффективно и точно изучать их свойства и применять их в различных областях математики и науки.