Как найти периметр шестиугольника
- Что такое периметр многоугольника
- Как найти периметр шестиугольника
- Пример вычисления периметра шестиугольника
- Периметр правильного шестиугольника
- Радиус описанной и вписанной окружностей
- Периметр по площади
Что такое периметр многоугольника
Периметром плоской фигуры называется длина её ограничивающей линии. Для нахождения периметра многоугольника нужно сложить длины всех его сторон. Если многоугольник является правильным, то задача нахождения периметра упрощается.
Как найти периметр шестиугольника
Чтобы найти периметр шестиугольника, нужно измерить и сложить длины всех его шести сторон. Формула для вычисления периметра шестиугольника выглядит следующим образом: P = a1 + a2 + a3 + a4 + a5 + a6, где P - периметр шестиугольника, а a1, a2 ... a6 - длины его сторон. Важно привести единицы измерения сторон к одному виду, чтобы можно было просто сложить числовые значения длин сторон.
Пример вычисления периметра шестиугольника
Допустим, у нас есть шестиугольник со сторонами 1 см, 2 мм, 3 мм, 4 мм, 5 мм и 6 мм. Чтобы найти его периметр, нужно привести единицы измерения к одному виду. Переведём 1 см в 10 мм. Затем сложим все длины сторон: 10 + 2 + 3 + 4 + 5 + 6 = 30 мм.
Периметр правильного шестиугольника
Если шестиугольник является правильным, то его периметр можно найти, умножив длину его стороны на шесть. Формула для вычисления периметра правильного шестиугольника выглядит так: P = a * 6, где a - длина стороны правильного шестиугольника.
Радиус описанной и вписанной окружностей
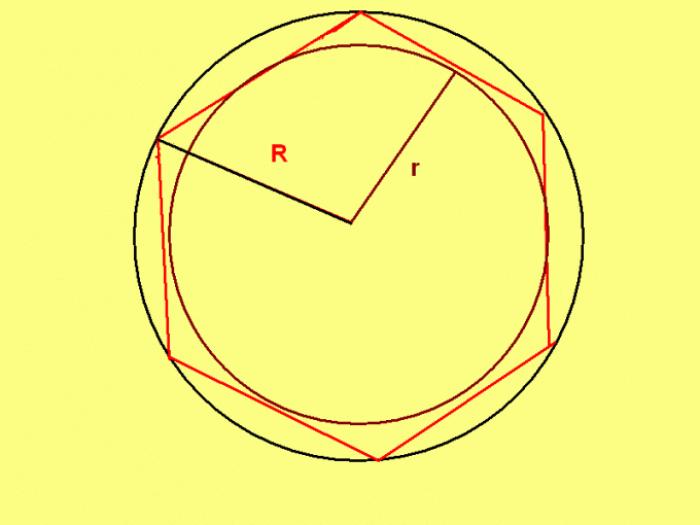
У правильного шестиугольника есть уникальное свойство: радиус описанной окружности равен длине его стороны. Если известен радиус описанной окружности, то периметр можно найти, умножив его на шесть. Формула выглядит так: P = R * 6, где R - радиус описанной окружности.
Если же известен радиус вписанной окружности, то формула для вычисления периметра выглядит следующим образом: P = 4 * √3 * r, где r - радиус вписанной в правильный шестиугольник окружности.
Периметр по площади
Если известна площадь правильного шестиугольника, то можно использовать следующую формулу для расчёта его периметра: P = 6 * √(2S√3), где S - площадь правильного шестиугольника.
Таким образом, существует несколько способов вычисления периметра шестиугольника в зависимости от известных данных. Используйте соответствующую формулу, чтобы найти периметр многоугольника.






