Как найти периметр восьмиугольника

Содержание:

1. Периметр восьмиугольника
2. Вычисление периметра при известных длинах сторон
3. Вычисление периметра при известном радиусе описанной окружности
4. Вычисление периметра при известном радиусе вписанной окружности
5. Вычисление периметра путем измерения

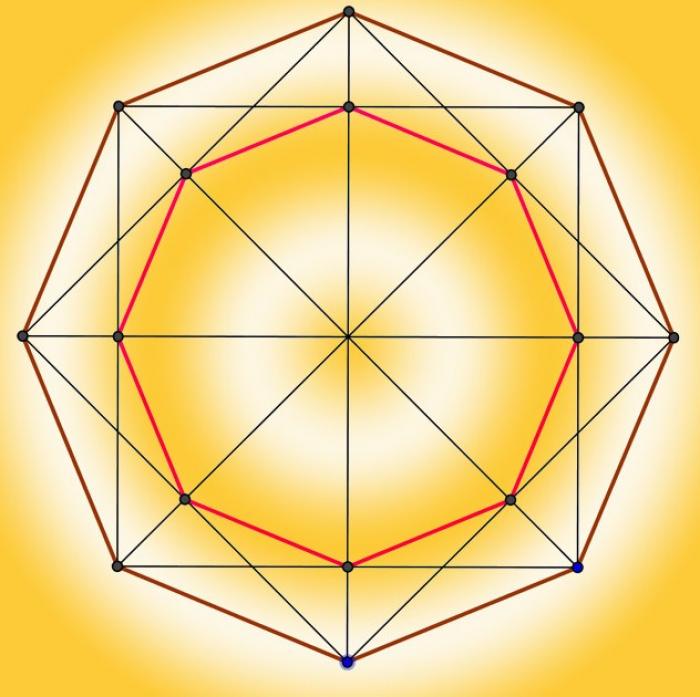
Периметр восьмиугольника

Периметром восьмиугольника, как и любой другой плоской геометрической фигуры, называют сумму длин его сторон. Решать задачу определения этого параметра многоугольника иногда приходится только с использованием математических формул, а иногда - измерять их какими-либо подручными средствами. В любом случае способов решения задачи существует несколько и каждый из них будет оптимален применительно к определенному набору исходных условий.

Вычисление периметра при известных длинах сторон

Если вычислить периметр (P) восьмиугольника надо в теории, а в исходных условиях даны длины всех сторон этой фигуры (a, b, c, d, e, f, g, h), то сложите эти величины: P = a+b+c+d+e+f+g+h. Знать длины всех сторон необходимо только в случае неправильного многоугольника, а если из условий задачи известно, что фигура является правильной, то будет достаточно длины одной стороны - просто увеличьте ее в восемь раз: P = 8*a.

Вычисление периметра при известном радиусе описанной окружности

Если в исходных данных ничего не говорится о длине стороны правильного восьмиугольника, но приведен радиус описанной около этой фигуры окружности (R), то перед применением формулы из предыдущего шага придется вычислить недостающую переменную. Каждую из сторон в таком восьмиугольнике можно считать основанием равнобедренного треугольника, боковыми сторонами которого являются радиусы описанной окружности. Поскольку всего таких одинаковых треугольников будет восемь, то величина угла между радиусами каждого из них составит одну восьмую часть от полного оборота: 360°/8 = 45°. Зная длины двух сторон треугольника и величину угла между ними, определите величину основания - косинус половины угла умножьте на удвоенную длину боковой стороны: 2*R*cos(22,5°) ≈ 2*R* 0,924 ≈ R* 1,848. Полученное значение подставьте в формулу из первого шага: P ≈ 8*R*1,848 ≈ R*14,782.

Вычисление периметра при известном радиусе вписанной окружности

Если в условиях задачи дан лишь радиус (r) вписанной в правильный восьмиугольник окружности, то надо произвести вычисления, аналогичные описанным выше. В этом случае радиус можно представить в качестве одного из катетов прямоугольного треугольника, другим катетом которого будет половина от нужной вам стороны восьмиугольника. Острый угол, примыкающий к радиусу, будет в два раза меньшее вычисленного в предыдущем шаге: 360°/16 = 22,5°. Длину нужного катета вычислите умножением тангенса этого угла на другой катет (радиус), а для определения величины стороны восьмиугольника полученное значение удвойте: 2*r*tg(22,5°) ≈ 2*r*0,414 ≈ r*0,828. Подставьте это выражение в формулу из первого шага: P ≈ 8*r*0,828 ≈ r*6,627.

Вычисление периметра путем измерения

Если вычислять радиус требуется методом практических измерений, то, в зависимости от размера фигуры, воспользуйтесь, например, линейкой, курвиметром («роликовым дальномером») или шагомером. Полученные значения длин сторон подставьте в одну из двух формул, приведенных в одном из шагов.