Как найти площадь поверхности прямоугольного параллелепипеда
- Что такое прямоугольный параллелепипед?
- Формула для расчета площади поверхности
- Как вычислить площади граней
- Расчет площади поверхности
- Прямоугольный параллелепипед и прямой параллелепипед
- Куб как частный случай прямоугольного параллелепипеда
Что такое прямоугольный параллелепипед?
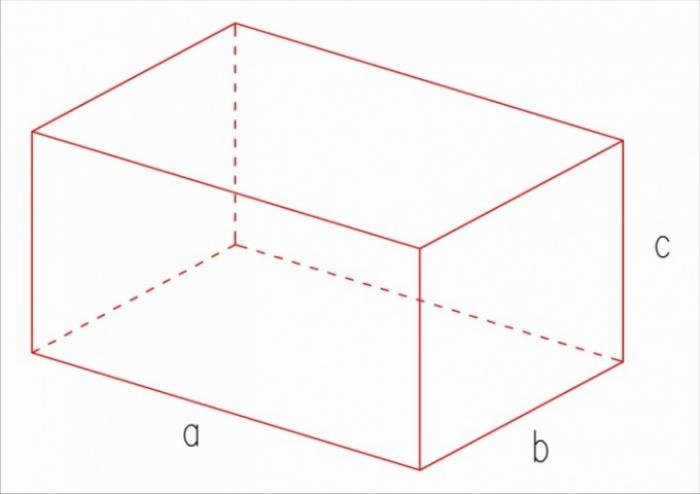
Прямоугольным называется такой параллелепипед, все шесть граней которого являются прямоугольниками. Этот геометрический объект имеет множество практических применений и широко используется в строительстве, инженерии и других отраслях.
Формула для расчета площади поверхности
Для вычисления площади поверхности прямоугольного параллелепипеда используется следующая формула: S = 2(ab + bc + ac), где a, b и c – длины ребер. Эта формула позволяет нам быстро и легко определить площадь поверхности параллелепипеда.
Как вычислить площади граней
Для начала необходимо вычислить площади трех разных граней параллелепипеда. Например, длина параллелепипеда (а) равна 7 см, ширина (b) – 6 см, а высота (с) – 4 см. Тогда площадь верхней (нижней) грани будет равна ab, т.е. 7х6=42 см. Площадь одной из боковых граней будет равна bc, т.е. 6х4=24 см. Наконец, площадь передней (задней) грани будет равна ac, т.е. 7х4=28 см.
Расчет площади поверхности
Теперь необходимо сложить вместе все три результата и умножить полученную сумму на два. В нашем примере это будет выглядеть следующим образом: 42+24+28=94; 94х2=188. Таким образом, площадь поверхности данного прямоугольного параллелепипеда будет равна 188 см.
Прямоугольный параллелепипед и прямой параллелепипед
Важно отметить, что прямоугольный параллелепипед отличается от прямого параллелепипеда. У прямого параллелепипеда прямоугольниками являются только боковые стороны (4 из 6-ти граней), а верхнее и нижнее основания – произвольные параллелограммы.
Куб как частный случай прямоугольного параллелепипеда
Куб является частным случаем прямоугольного параллелепипеда. Так как все его грани равны, то для нахождения его поверхности будет необходимо возвести длину ребра в квадрат и умножить на 6. Кубы также широко используются в архитектуре и дизайне благодаря своей симметричной форме и удобной геометрии.
В конечном итоге, знание формулы для расчета площади поверхности прямоугольного параллелепипеда может быть очень полезным в различных сферах нашей жизни. Этот простой математический инструмент позволяет точно определить площадь поверхности объекта и применить это знание в практике.