Как найти площадь прямоугольной призмы
- Определение призмы и ее основания
- Площадь оснований призмы
- Площадь боковой поверхности призмы
- Общая площадь поверхности призмы
- Заключение
Определение призмы и ее основания
Призма - это многогранник, две грани которого являются равными многоугольниками с соответственно параллельными сторонами, а остальные грани - параллелограммы. Однако, для определения площади поверхности призмы необходимо знать какая фигура является ее основанием.
Площадь оснований призмы
Призма может иметь различные формы основания, включая треугольное, четырехугольное, пятиугольное и т.д. В данном случае, по условию, призма является прямоугольной, что означает, что ее основаниями являются прямоугольники. Площадь прямоугольника определяется как произведение длин его сторон. Таким образом, площадь одного основания призмы равна ab, а так как призма имеет два равных основания, их суммарная площадь будет 2ab.
Площадь боковой поверхности призмы
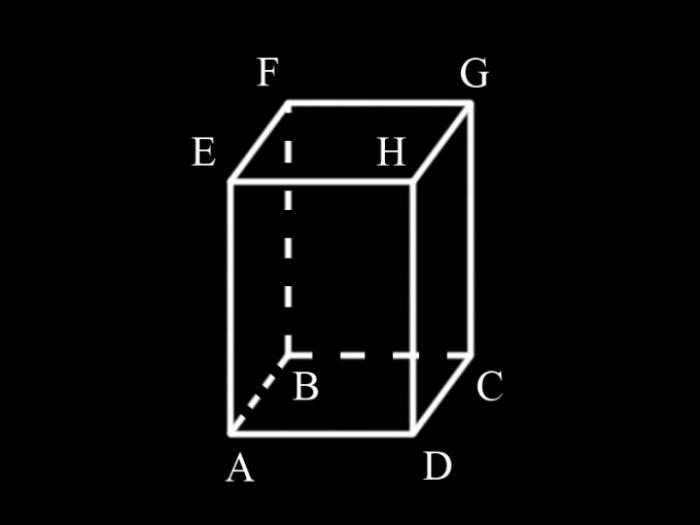
Призма имеет 4 боковые грани, которые также являются прямоугольниками. Для определения их площади необходимо знать длину сторон оснований (a и b) и высоту призмы (h). Одна из боковых граней имеет сторону AD, которая также является стороной основания ABDC и равна а. Также, боковая грань имеет сторону AE, которая является высотой призмы и равна h. Таким образом, площадь одной боковой грани равна ah. Поскольку призма имеет 4 боковые грани, их суммарная площадь будет 2ah.
Общая площадь поверхности призмы
Таким образом, площадь боковой поверхности призмы равна сумме площадей ее боковых граней, то есть 2ah. Для определения общей площади поверхности призмы необходимо сложить площадь оснований (2ab) и площадь боковой поверхности (2ah). Итак, общая площадь поверхности призмы равна 2(ab + ah).
Заключение
Таким образом, для определения площади поверхности прямоугольной призмы необходимо знать длины сторон ее оснований (a и b) и ее высоту (h). Общая площадь поверхности призмы равна 2(ab + ah). Эта формула может быть использована для решения задач по определению площади поверхности призмы.