Как найти площадь сечения шара
- Нахождение площади сечения шара плоскостью
- Крайние случаи и границы площади
- Таким образом, получаем границы площади: 0 < S < πR^2.
- Нахождение радиуса окружности сечения
- Вывод радиуса окружности сечения
- Вычисление площади сечения
Нахождение площади сечения шара плоскостью
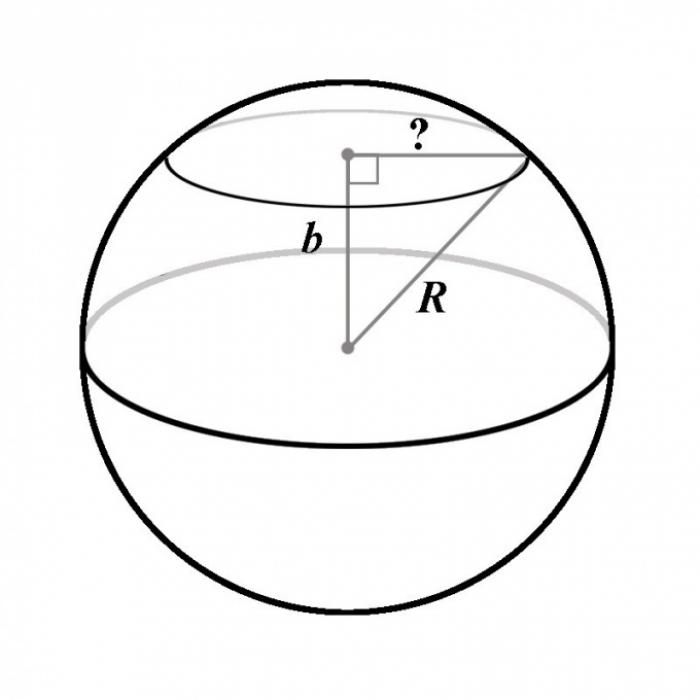
Дан шар с радиусом R, который пересекает плоскость на расстоянии b от его центра. Нам требуется найти площадь сечения, образованного при этом.
Крайние случаи и границы площади
Рассмотрим два крайних случая: если расстояние b равно радиусу шара R, то плоскость касается шара только в одной точке, и площадь сечения будет равна нулю, т.е. S = 0. Если же расстояние b равно нулю, то плоскость проходит через центр шара, и сечение будет представлять собой круг с радиусом R. Площадь этого круга можно вычислить по формуле S = πR^2.
Таким образом, получаем границы площади: 0 < S < πR^2.
Нахождение радиуса окружности сечения
Любое сечение шара плоскостью будет всегда кругом. Поэтому, чтобы найти площадь сечения, мы должны сначала найти радиус этой окружности.
Вывод радиуса окружности сечения
Расстояние от точки до плоскости определяется как длина отрезка, перпендикулярного плоскости и начинающегося в этой точке. В данном случае, второй конец этого отрезка совпадает с центром окружности сечения. Такой вывод следует из определения шара: все точки окружности сечения принадлежат сфере и, следовательно, находятся на равном расстоянии от центра шара.
Это означает, что каждая точка окружности сечения может рассматриваться как вершина прямоугольного треугольника, гипотенузой которого является радиус шара, одним из катетов - перпендикулярный отрезок, соединяющий центр шара с плоскостью, а вторым катетом - радиус окружности сечения.
Используя известные значения двух сторон этого треугольника - радиус шара R и расстояние b, по теореме Пифагора можно вычислить длину второго катета, который равен √(R^2 - b^2). Это и будет радиусом окружности сечения.
Вычисление площади сечения
Подставляя найденное значение радиуса в формулу площади круга S = πR^2, мы можем легко получить формулу для вычисления площади сечения шара плоскостью: S = π(R^2 - b^2). Эта формула полностью согласуется с уже найденными результатами в частных случаях, когда b = R или b = 0.
