Как найти площадь трапеции, если известны основания
- Определение трапеции
- Нахождение площади трапеции по известным значениям
- Пример нахождения площади трапеции
- Равнобедренная трапеция
Определение трапеции
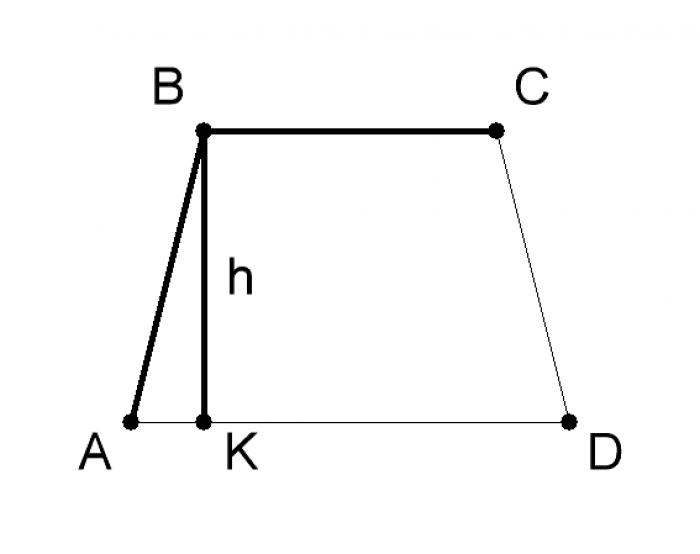
Трапеция - это четырехугольник, у которого только одна пара сторон параллельна. Основания трапеции - это пара параллельных сторон. Расстояние между основаниями называется высотой трапеции.
Нахождение площади трапеции по известным значениям
Для нахождения площади трапеции используются геометрические формулы. Если известны длины оснований и высоты трапеции, можно использовать формулу S = 1/2 (a+b)*h, где a и b - длины оснований, h - высота.
Пример нахождения площади трапеции
Допустим, основание AD (a) трапеции составляет 10 см, основание BC (b) - 6 см, высота BK (h) - 8 см. Подставляя эти значения в формулу, получаем: S = 1/2 (10+6)*8 = 1/2 * 16 * 8 = 64 кв.см.
Нахождение площади трапеции с известными основаниями и боковыми сторонами
Если помимо оснований известны также боковые стороны трапеции, можно использовать формулу S = (a+b)/2*(√(c^2 - ((b-a)^2+c^2-d^2)/(2(b-a))^2), где a и b - длины оснований, c и d - длины боковых сторон.
Пример нахождения площади трапеции с известными основаниями и боковыми сторонами
Предположим, основание AD (a) равно 10 см, основание BC (b) - 6 см, сторона AB (c) - 9 см и сторона CD (d) - 8 см. Подставляя эти значения в формулу и упрощая выражение, получаем: S = (10+6)/2*(√(9^2 - ((10-6)^2+9^2-8^2)/(2(10-6))^2) = 64 кв.см.
Равнобедренная трапеция
Если две боковые стороны трапеции равны, она называется равнобедренной. У такой трапеции диагонали равны между собой, а также равны углы при основании.






