Как найти площадь треугольника по двум сторонам
- Как вычислить площадь треугольника при заданных сторонах
- Необходимые инструменты
- Шаг 1: Измерьте угол между сторонами
- Шаг 2: Вычислите площадь треугольника
- Шаг 3: Вычисление синуса угла
- Дополнительные возможности
- Шаг 4: Вычислите площадь треугольника
- Заключение
Как вычислить площадь треугольника при заданных сторонах
Иногда в жизни возникают ситуации, когда нам необходимо знание геометрии. Хотя такая информация редко используется в повседневной жизни, но существуют вопросы, которые требуют наличия этих знаний. Один из таких вопросов - как найти площадь треугольника, если известны длины двух его сторон.
Необходимые инструменты
Для вычисления площади треугольника вам понадобятся следующие инструменты: линейка, транспортир и калькулятор.
Шаг 1: Измерьте угол между сторонами
Для вычисления площади треугольника, необходимо измерить угол между двумя сторонами. Для этого воспользуйтесь транспортиром или другим инструментом для измерения углов. Например, малка может быть очень удобной для измерения углов в комнате.
Шаг 2: Вычислите площадь треугольника
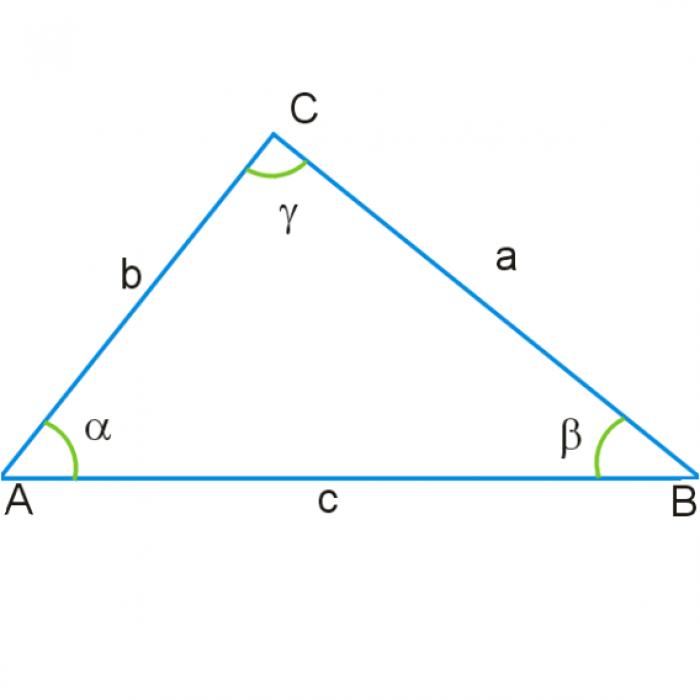
После того, как вы определили длины двух сторон треугольника и измерили угол между ними, можно приступить к вычислениям. Формула для вычисления площади треугольника при известных сторонах и угле между ними выглядит следующим образом: S∆ abc = 1/2 ab sin угла. Если у вас есть прямой угол между двумя известными сторонами треугольника, то формулу можно упростить: S∆ abc = 1/2 ab.
Шаг 3: Вычисление синуса угла
Для вычисления синуса угла можно воспользоваться тригонометрической таблицей Брадиса, где приведены значения синуса для наиболее распространенных углов. Также вы можете использовать калькулятор. Если у вас есть операционная система Windows, в ней уже есть калькулятор с режимом "Инженерный", который позволяет вычислять синус угла. Просто откройте калькулятор, переключитесь в режим "Инженерный" и введите размер угла, синус которого хотите вычислить. Выберите единицы измерения для результата и нажмите кнопку "sin", чтобы получить результат.
Дополнительные возможности
Если вам необходимо вычислить синус угла с более сложным интерфейсом или расширенными возможностями, вы можете воспользоваться онлайн-калькулятором тригонометрических функций. В Интернете существует множество подобных программ, достаточно найти их с помощью поисковика. Просто введите запрос "калькулятор тригонометрических функций".
Шаг 4: Вычислите площадь треугольника
Теперь у вас есть все необходимые данные: длины двух сторон треугольника и значение синуса угла между ними. Перемножьте длины сторон и синус угла, разделите результат на 2 и вы получите площадь треугольника.
Заключение
Треугольник состоит из трех сторон, соединяющих три точки, не лежащих на одной прямой. Вычисление площади треугольника может быть полезным в различных ситуациях, и знание геометрии позволяет решать подобные задачи.