Как найти производную корня
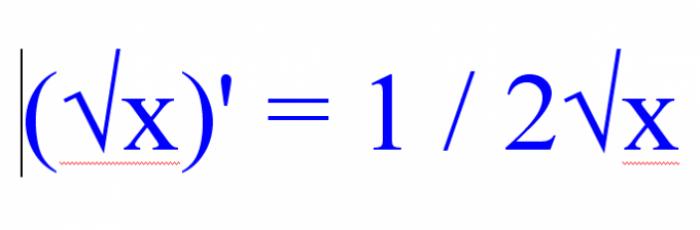
- Как найти производную корня в математическом анализе
- Инструкция по нахождению производной корня
- Правила для производных степенных функций
- Упрощение выражений после дифференцирования
- Нахождение производной корня вместе с другими функциями
- Онлайн инструменты для вычисления производных
- Заключение
Как найти производную корня в математическом анализе
В задачах по математическому анализу иногда возникает необходимость найти производную корня. В зависимости от условий задачи, производная от функции "корень квадратный" или "корень кубический" может быть найдена непосредственно или с помощью преобразования корня в степенную функцию с дробным показателем.
Инструкция по нахождению производной корня
Перед тем как находить производную корня, необходимо обратить внимание на остальные функции, присутствующие в примере. Если в задаче присутствует много подкоренных выражений, то для нахождения производной квадратного корня применяется правило (√х)' = 1 / 2√х, а для нахождения производной кубического корня используется формула (³√х)' = 1 / 3(³√х)².
Если в примере, предназначенном для дифференцирования, встречается переменная в дробных степенях, то корень переводится в степенную функцию с соответствующим показателем. Для квадратного корня это будет степень ½, а для кубического корня – ⅓: √х = х ^ ½, ³√х = x ^ ⅓.
Правила для производных степенных функций
Для нахождения производной степенной функции в общем случае и для х^½, x^⅓ в частности используется правило (х ^ n)' = n * x^(n-1). Для производной корня из этого соотношения получаем (х^½)' = ½ x ^ (-½) и (x^⅓)' = ⅓ x ^ (-⅔).
Упрощение выражений после дифференцирования
После дифференцирования всех корней, следует внимательно рассмотреть остальные части примера. Если в ответе получается сложное выражение, то вероятно его можно упростить. Большинство школьных примеров составлено таким образом, чтобы в итоге получить компактное выражение или небольшое число.
Нахождение производной корня вместе с другими функциями
Во многих задачах на нахождение производной корни встречаются вместе с другими функциями. Для нахождения производной корня в таких случаях применяются следующие правила:
- Производная константы равна нулю: C' = 0.
- Постоянный множитель выносится за знак производной: (k*f)' = k * (f)'.
- Производная суммы нескольких функций равна сумме производных: (f + g)' = (f)' + (g)'.
- Производная произведения двух функций равна (f)'g + f(g)'.
- Производная частного равна ((f)'g – f(g)') / g².
Онлайн инструменты для вычисления производных
На многих онлайн платформах предоставляются инструменты для вычисления производной функции с получением подробного решения задачи. Эти инструменты основаны на правилах дифференцирования, которые студенты изучают в курсе математического анализа.
Чтобы найти производную функции, необходимо ввести функцию в соответствующее поле и следовать правилам ввода данных.
Заключение
Нахождение производной корня может быть необходимо в задачах по математическому анализу. Для этого используются различные правила и формулы, которые позволяют найти производную как непосредственно, так и путем преобразования корня в степенную функцию. Важно также упрощать выражения после дифференцирования и применять правила для нахождения производных вместе с другими функциями. Онлайн инструменты могут значительно облегчить процесс вычисления производных функций.






