Как найти радиус по хорде
- Как найти радиус окружности, зная длину хорды и угол между радиусами?
- Шаг 1: Известные данные
- Шаг 2: Решение задачи
- R = (AB/2) / sin(x/2)
- Вывод
Как найти радиус окружности, зная длину хорды и угол между радиусами?
Хорда - это отрезок, соединяющий две точки на окружности. Если нам известна длина хорды и угол между радиусами, проведенными в концы хорды, мы можем найти радиус окружности. Для этого нам понадобятся транспортир и линейка.
Шаг 1: Известные данные
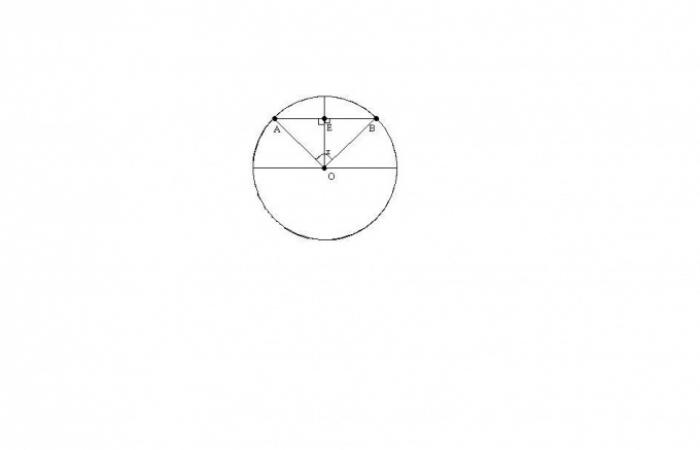
Пусть у нас есть хорда AB длиной AB и угол AOB между радиусами, проведенными в концы хорды.
Шаг 2: Решение задачи
Треугольник AOB является равнобедренным, так как OA = OB = R (радиус окружности). Согласно свойствам равнобедренного треугольника, высота OE одновременно является его медианой и биссектрисой угла AOB.
Обозначим угол AOB за x. Треугольник AEO прямоугольный, с прямым углом AEO. Учитывая, что высота OE также является биссектрисой угла AOB, получаем, что угол AOE равен x/2.
Из прямоугольного треугольника AOE мы можем найти радиус окружности R. Формула для нахождения радиуса будет следующей:
R = (AB/2) / sin(x/2)
Вывод
Итак, зная длину хорды и угол между радиусами, мы можем легко вычислить радиус окружности. Для этого мы использовали свойства равнобедренного треугольника и прямоугольного треугольника. Эта информация пригодится нам, когда мы будем работать с окружностями и хордами в геометрии.