Как найти синус угла по сторонам треугольника
- Базовые варианты нахождения синусов углов в треугольнике
- Нахождение синусов углов в прямоугольном треугольнике
- Нахождение синусов углов в произвольном треугольнике
- Нахождение синуса угла через формулу площади треугольника
Базовые варианты нахождения синусов углов в треугольнике
Синус - это одна из базовых тригонометрических функций, которая была выведена из соотношений длин сторон в прямоугольном треугольнике. Для прямоугольного треугольника существуют базовые определения синусов углов, а для произвольных треугольников применяется теорема косинусов.
Нахождение синусов углов в прямоугольном треугольнике
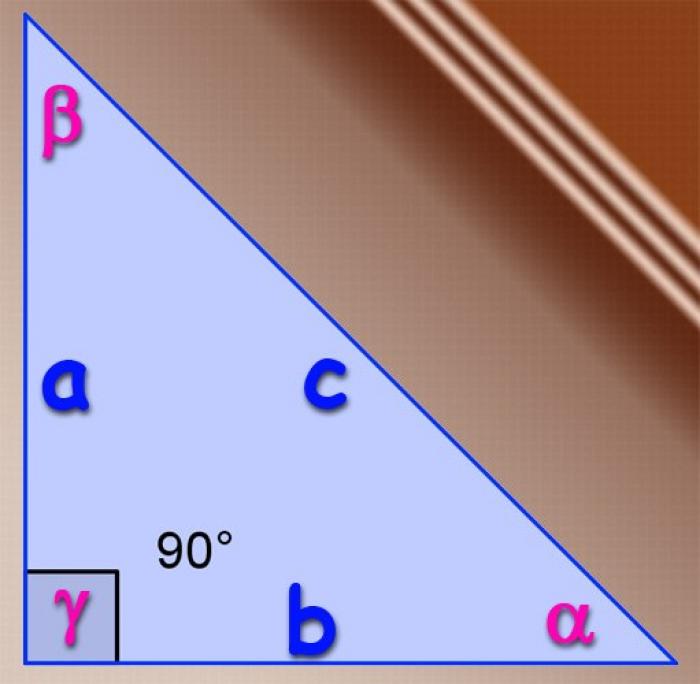
Если рассматриваемый треугольник является прямоугольным, то можно использовать базовое определение тригонометрической функции синуса для острых углов. Синусом угла называется соотношение длины катета, лежащего напротив этого угла, к длине гипотенузы. Для угла α, лежащего напротив катета А, синус определяется по формуле α=А/С, а для угла β, лежащего напротив катета В, синус определяется по формуле β=В/С. В прямоугольном треугольнике нет необходимости находить синус третьего угла, так как он всегда равен единице.
Нахождение синусов углов в произвольном треугольнике
Для нахождения синусов углов в произвольном треугольнике используется теорема косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С²-2*В*С*cos(α).
Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С). А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С)²).
Нахождение синуса угла через формулу площади треугольника
Для нахождения синуса угла в произвольном треугольнике можно также использовать формулы для расчета площади треугольника. Формула Герона, которая использует только длины сторон треугольника, выглядит так: S=¼*√((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)).
Формула для расчета площади треугольника через длины двух сторон и синус угла между ними выглядит так: S=А*В*sin(γ). Подставляя первую формулу во вторую, можно получить формулу для нахождения синуса угла γ, лежащего напротив стороны С: sin(γ)= ¼*√((А+В+С)*(В+С-А)*(А+С-В)*(А+В-С)/(А*В)). Синусы двух других углов можно найти по аналогичным формулам.






