Как найти синус угла в равнобедренном треугольнике
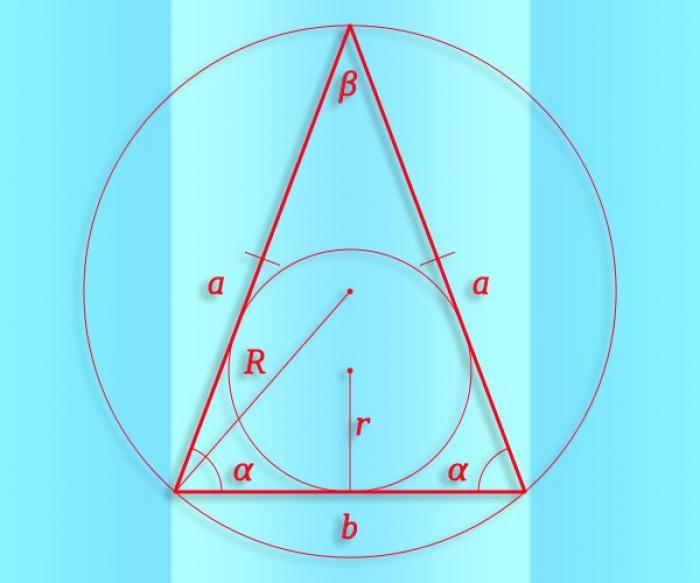
- Равнобедренный треугольник
- Известный угол
- Окружность, описанная вокруг треугольника
- Площадь и длина стороны
- Длина стороны и основание
Равнобедренный треугольник
Равнобедренным треугольником называется геометрическая фигура, у которой две стороны имеют одинаковую длину. Этот вид треугольника имеет особые свойства, которые позволяют рассчитать синусы углов в нем, используя различные формулы.
Известный угол
Если в равнобедренном треугольнике известна величина одного угла, это позволяет найти два других и, следовательно, синус любого из них. Используя теорему о сумме углов в треугольнике, можно найти углы, лежащие между боковыми сторонами, а также углы, примыкающие к основанию треугольника.
Окружность, описанная вокруг треугольника
Если известны радиус окружности, описанной вокруг равнобедренного треугольника, и длина любой из его сторон, можно рассчитать синус угла, лежащего напротив этой стороны. Используя теорему синусов, можно выразить синус угла как половину отношения длины стороны к радиусу окружности.
Площадь и длина стороны
Известные значения площади и длины боковой стороны равнобедренного треугольника позволяют рассчитать синус угла, лежащего напротив основания треугольника. Для этого необходимо удвоить площадь и разделить полученное значение на квадрат длины боковой стороны. Если известна также длина основания, квадрат можно заменить произведением длин основания и боковой стороны.
Длина стороны и основание
Если известны длины боковой стороны и основания равнобедренного треугольника, можно использовать теорему косинусов для вычисления синуса угла при основании. Зная, что косинус этого угла равен половине отношения длины основания к длине боковой стороны, можно выразить синус через косинус и вычислить его, используя соотношение между синусом и косинусом.
Таким образом, синусы углов в равнобедренном треугольнике могут быть вычислены с использованием различных формул, основанных на известных значениях углов, длин сторон, радиуса окружности и площади треугольника. Это позволяет более точно определить геометрические характеристики и свойства такого треугольника.
