Как найти среднюю линию равнобедренной трапеции
- Что такое трапеция?
- Расчет средней линии трапеции
- Расчет по длине оснований
- Расчет по площади и высоте
- Расчет по периметру и длине боковой стороны
- Расчет по периметру, высоте и углу
Что такое трапеция?
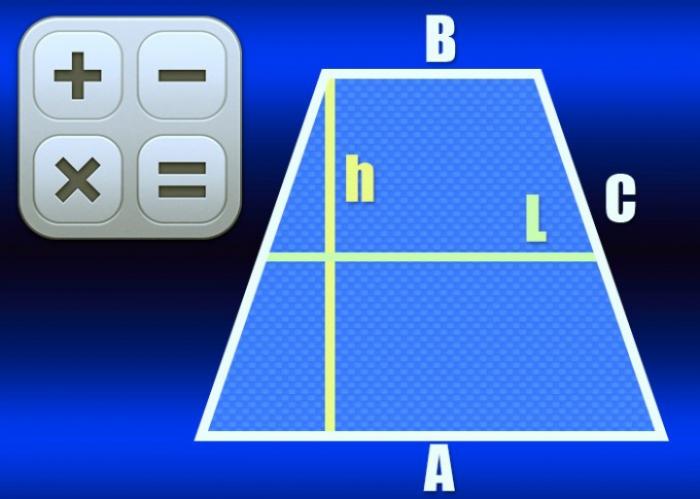
Трапецией называется четырехугольник, у которого есть две параллельные стороны, называемые основаниями. Если боковые стороны трапеции имеют одинаковую длину, то такая фигура называется равнобедренной или равнобокой.
Расчет средней линии трапеции
Средняя линия трапеции - это линия, соединяющая середины боковых сторон. Ее длину можно рассчитать несколькими способами, в зависимости от известных параметров.
Расчет по длине оснований
Если известны длины обоих оснований (А и В) трапеции, то для вычисления длины средней линии (L) можно использовать следующую формулу: L = ½*(А+В).
Пример: если длины оснований равны 10 см и 20 см, то средняя линия будет равна ½*(10+20) = 15 см.
Расчет по площади и высоте
Если известны площадь (S) и высота (h) равнобокой трапеции, то можно вычислить длину средней линии (L) по следующей формуле: L = S/h.
Пример: при площади 75 см² и высоте 15 см, средняя линия будет равна 75/15 = 5 см.
Расчет по периметру и длине боковой стороны
Если известны периметр (P) и длина боковой стороны (С) равнобокой трапеции, то можно вычислить длину средней линии (L) по следующей формуле: L = (P-2*С)/2.
Пример: при периметре 150 см и длине боковой стороны 25 см, длина средней линии будет равна (150-2*25)/2 = 50 см.
Расчет по периметру, высоте и углу
Если известны периметр (P), высота (h) и величина одного из острых углов (α) равнобокой трапеции, то можно вычислить длину средней линии (L) по следующей формуле: L = P/2-h/sin(α).
Пример: если известный угол имеет величину 30°, высота равна 10 см, а периметр составляет 150 см, то длина средней линии будет равна 150/2-10/sin(30°) = 75-20 = 55 см.
Теперь вы знаете несколько способов вычисления длины средней линии равнобокой трапеции. Эти формулы помогут вам в решении задач, связанных с этой геометрической фигурой.
