Как найти сторону трапеции, если известно основание
- Трапеция - геометрическая фигура с четырьмя углами
- Задача 1: Нахождение боковой стороны равнобедренной трапеции
- Шаг 1: Опускаем перпендикуляр
- Шаг 2: Находим AE
- Шаг 3: Находим AB
- Задача 2: Нахождение боковой стороны трапеции с известной высотой
- Шаг 1: Проводим вторую высоту
- Шаг 2: Находим CD
- Шаг 3: Находим AB
Трапеция - геометрическая фигура с четырьмя углами
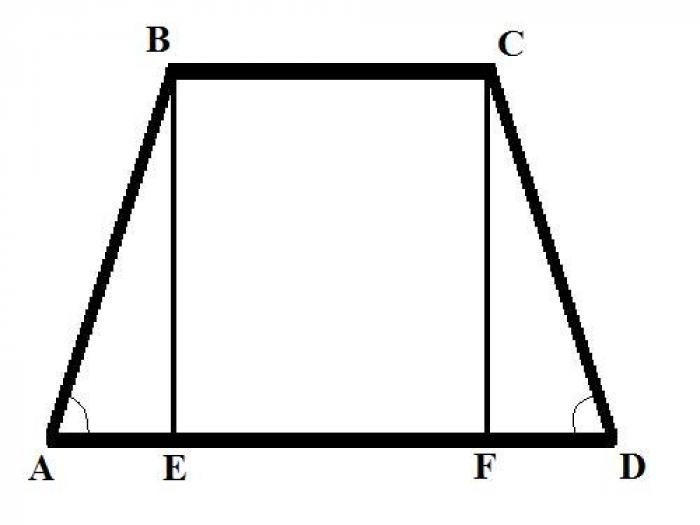
Трапеция - это геометрическая фигура, которая имеет четыре угла. Она состоит из двух параллельных сторон, которые называются основаниями, и двух других сторон, которые не параллельны и называются боковыми.
Задача 1: Нахождение боковой стороны равнобедренной трапеции
В этой задаче мы рассмотрим ситуацию, когда нам известны основания трапеции (BC = b, AD = d), угол при боковой стороне (BAD) и мы должны найти длину боковой стороны.
Шаг 1: Опускаем перпендикуляр
Нам нужно опустить перпендикуляр (высоту трапеции) из вершины B до пересечения с большим основанием. Пусть этот перпендикуляр пересекается с большим основанием в точке E. Тогда длина отрезка AB может быть выражена через угол BAD: AB = AE/cos(BAD) = AE/cos(Альфа).
Шаг 2: Находим AE
Длина отрезка AE равна разности длин двух оснований, деленной пополам: AE = (AD - BC)/2 = (d - b)/2.
Шаг 3: Находим AB
Используя найденное значение AE, мы можем найти AB: AB = (d - b)/(2*cos(Альфа)). Для равнобедренной трапеции, длина боковой стороны CD также равна AB: CD = AB = (d - b)/(2*cos(Альфа)).
Задача 2: Нахождение боковой стороны трапеции с известной высотой
В этой задаче мы рассмотрим ситуацию, когда нам известны основания трапеции (BC = b, AD = d), высота (BE = h) и угол при противоположной боковой стороне (CDA). Наша цель - найти длину боковой стороны AB.
Шаг 1: Проводим вторую высоту
Нам нужно провести вторую высоту из вершины C до пересечения с нижним основанием. Пусть этот перпендикуляр пересекается с нижним основанием в точке F. Тогда длина отрезка FD может быть выражена через угол CDA: FD = CD*cos(CDA).
Шаг 2: Находим CD
Длина боковой стороны CD может быть найдена из следующей формулы: CD = CF/sin(CDA). Используя то, что CF = BE = h, мы можем записать FD = h*cos(Альфа)/sin(Альфа) = h*ctg(Альфа).
Шаг 3: Находим AB
Рассмотрим прямоугольный треугольник ABE. Зная длины его сторон AE и BE, мы можем найти третью сторону - гипотенузу AB. Длина стороны AE может быть найдена следующим образом: AE = AD - BC - FD = d - b - h*ctg(Альфа). Используя свойство прямоугольного треугольника, где квадрат гипотенузы равен сумме квадратов катетов, мы можем выразить AB: AB^2 = h^2 + (d - b - h*ctg(Альфа))^2. Окончательно, длина боковой стороны трапеции AB равна квадратному корню из этого выражения.
