Как найти стороны прямоугольного треугольника
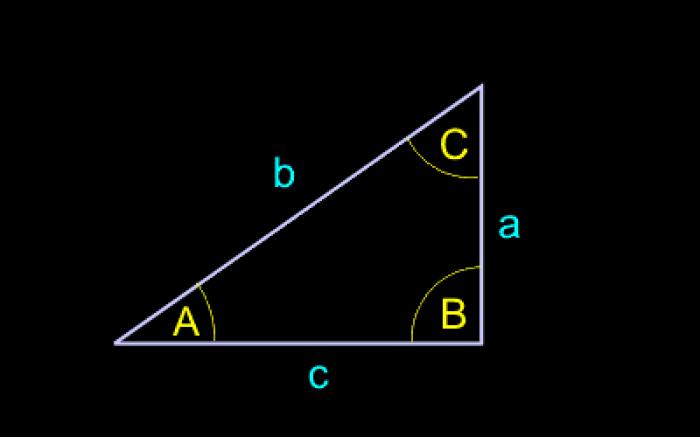
- Тригонометрия: нахождение сторон прямоугольного треугольника
- Нахождение сторон с известными гипотенузой и одним катетом
- Нахождение сторон с известными обоими катетами
- Нахождение сторон с известным углом и гипотенузой
- Нахождение сторон с известным углом и одним катетом
- Полезные советы
Тригонометрия: нахождение сторон прямоугольного треугольника
Тригонометрия - раздел математики, который изучает соотношения между сторонами и углами прямоугольного треугольника. Для решения задач на нахождение сторон прямоугольного треугольника необходимо знать теорему Пифагора, определения тригонометрических функций и иметь средства для нахождения их значений, такие как калькулятор или таблицы Брадиса.
Нахождение сторон с известными гипотенузой и одним катетом
Если известны гипотенуза (с) и один из катетов (а), то второй катет можно вычислить с помощью теоремы Пифагора: b = sqrt(с^2 - а^2).
Нахождение сторон с известными обоими катетами
Если известны оба катета (а и b), то гипотенузу можно найти с помощью теоремы Пифагора: с = sqrt(а^2 + b^2).
Нахождение сторон с известным углом и гипотенузой
Если известен один из острых углов (A) и гипотенуза (с), то катеты можно вычислить, используя определения основных тригонометрических функций: a = c*sin(A), b = c*cos(A).
Нахождение сторон с известным углом и одним катетом
Если известен один из острых углов (A) и один из катетов (а), то гипотенуза и другой катет можно вычислить с помощью следующих соотношений: b = a*tg(A), c = a*sin(A).
Полезные советы
Если вам неизвестны значения синуса или косинуса необходимых для расчета углов, вы можете воспользоваться таблицами Брадиса, где указаны значения тригонометрических функций для множества углов. Также современные калькуляторы обычно имеют функции для расчета синусов и косинусов углов.
