Как найти стороны прямоугольного треугольника по площади

Содержание:

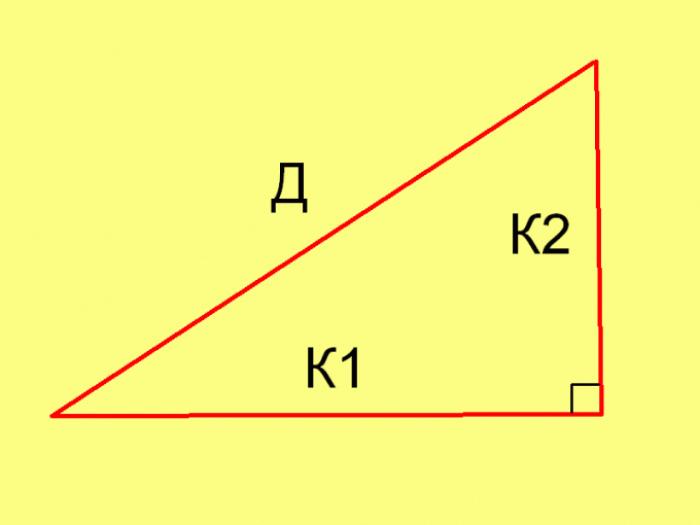
1. Нахождение площади прямоугольного треугольника
2. Нахождение сторон прямоугольного треугольника по площади
3. Обоснование формул
4. Пример вычислений
5. Пример вычислений
6. Пример вычислений

Нахождение площади прямоугольного треугольника

В некоторых задачах по геометрии требуется найти площадь прямоугольного треугольника, если известны длины его сторон. Так как длины сторон прямоугольного треугольника связаны теоремой Пифагора, а его площадь равна половине произведения длин катетов, то для решения этой задачи достаточно знать длины двух его любых сторон.

Нахождение сторон прямоугольного треугольника по площади

Если же нужно решить обратную задачу – найти стороны прямоугольного треугольника по его площади, то потребуется дополнительная информация. Для этого можно воспользоваться формулами К = √(2*Пл) или К = √2*√Пл и Д = 2*√Пл, где Пл – площадь треугольника, К – длина катета треугольника, Д – длина его гипотенузы. Длины сторон будут выражаться в соответствующих площади линейных единицах измерения.

Обоснование формул

Площадь равнобедренного прямоугольного треугольника: Пл = ½ * К², значит К² = 2 * Пл. Теорема Пифагора для равнобедренного прямоугольного треугольника: Д²=2 * К², значит Д = √2 * К.

Пример вычислений

Пусть, например, площадь равнобедренного прямоугольного треугольника равняется 25 см². В этом случае, длина его катетов будет равняться: К = √2 * √25 = 5√2, а длина гипотенузы: Д = 2 * √25 = 10.

Нахождение сторон прямоугольного треугольника по площади (общий случай)

Для нахождения длин сторон прямоугольного треугольника по его площади в общем случае, необходимо уточнить значение какого-либо из дополнительных параметров, таких как соотношение катетов, соотношение катета и гипотенузы, один из острых углов треугольника, длина одной из сторон или его периметр. Для расчета длин сторон в каждом конкретном случае используется теорема Пифагора и следующее равенство: Пл = ½ * К1 * К2, где К1 и К2 – длины катетов. Отсюда вытекает, что: К1 = 2Пл / К2 и, наоборот, К2 = 2Пл / К1.

Пример вычислений

Например, если соотношение катетов прямоугольного треугольника (К1/К2) равно 2, то К1 = √(2*2*25) = 10, К2 = 10/2 = 5 и Д = √(10²+5²) = √125.

Нахождение сторон прямоугольного треугольника по площади и другим параметрам

Аналогичным образом можно найти длины сторон прямоугольного треугольника, если известны площадь и другие параметры, такие как периметр. Для этого можно использовать систему уравнений: К1 + К2 + Д = Пе, К1² + К2² = Д² и К1 * К2 = 2Пл. Решив данную систему уравнений, можно определить длины сторон треугольника.

Пример вычислений

Пусть, например, известны площадь треугольника (Пл) и его периметр (Пе). Если Пл = 6 и Пе = 12, то получается система уравнений: К1+К2+Д = 12, К1² + К² = Д² и К1 * К2 = 12. Решив данную систему, можно узнать, что длины сторон треугольника равны 3, 4, 5.