Как найти сумму вектора
- Роль векторов в физике
- Сложение векторов
- Правило параллелограмма
- Противоположные векторы
- Разность векторов
- Свойства операции сложения векторов
- Операция сложения векторов обладает следующими свойствами:
Роль векторов в физике
Векторы играют важную роль в физике, поскольку они позволяют наглядно представить силы, действующие на тела. Для решения задач, связанных с механикой, необходимо знание векторов. В данной статье мы рассмотрим основные операции с векторами и их свойства.
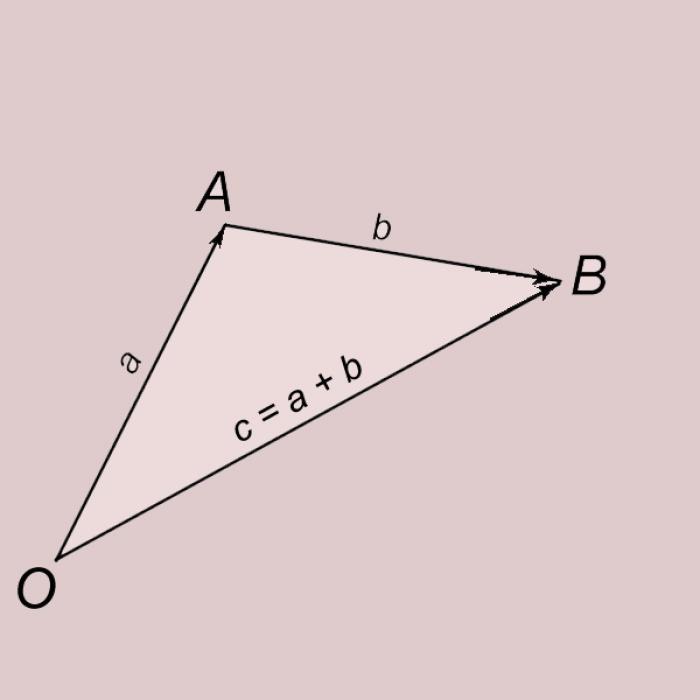
Сложение векторов
Сложение векторов выполняется по правилу треугольника. Пусть у нас есть два ненулевых вектора a и b. Отложим вектор a от точки O и обозначим его конец буквой A. Отложим от точки A вектор b и обозначим его конец буквой B. Вектор, начинающийся в точке O и заканчивающийся в точке B (OB = c), называется суммой векторов a и b и обозначается c = a + b.
Правило параллелограмма
Сумму двух неколлинеарных векторов a и b можно построить по правилу параллелограмма. Отложим от точки A векторы AB = b и AD = a. Через конец вектора a проведем прямую, параллельную вектору b, а через конец вектора b – прямую, параллельную вектору a. Пусть C – точка пересечения построенных прямых. Вектор AC = c – сумма векторов a и b. c = a + b.
Противоположные векторы
Вектором, противоположным вектору a, называют вектор, обозначаемый -a, такой, что сумма вектора a и вектора -a равна нулевому вектору: a + (-a) = 0. Вектор, противоположный вектору AB, обозначается также BA: AB + BA = AA = 0. Противоположные векторы имеют равные длины (|a| = |-a|) и противоположные направления.
Разность векторов
Суммой вектора a и вектора, противоположного вектору b, называют разность двух векторов a - b, то есть вектор a + (-b). Разность двух векторов a и b обозначается a - b. Разность двух векторов a и b может быть получена с помощью правила треугольника. Отложим от точки A вектор a. AB = a. От конца вектора AB отложим вектор BC = -b, вектор AC = c – разность векторов a и b. c = a - b.
Свойства операции сложения векторов
Операция сложения векторов обладает следующими свойствами:
- Свойство нулевого вектора: a + 0 = a.
- Ассоциативность сложения: (a + b) + c = a + (b + c).
- Коммутативность сложения: a + b = b + a.






