Как найти тангенс угла в треугольнике
- Тангенс угла и его вычисление
- Измерение тангенса угла
- Вычисление тангенса угла
- Особенности тангенса угла
- Изменение тангенса угла
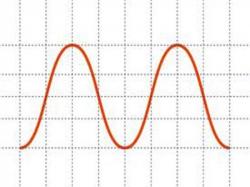
- График функции Y=tg(x)
Тангенс угла и его вычисление
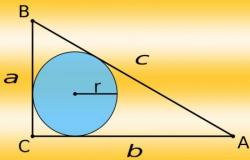
Тангенс угла, как и другие тригонометрические функции, выражает зависимость между сторонами и углами прямоугольного треугольника. Применение тригонометрических функций позволяет заменить в расчетах величины в градусном измерении на линейные параметры.
Измерение тангенса угла
При наличии транспортира заданный угол треугольника можно измерить и по таблице Брадиса найти значение тангенса. Если нет возможности определить градусную величину угла, определите его тангенс с помощью замеров линейных величин фигуры.
Для этого сделайте вспомогательные построения: из произвольной точки на одной из сторон угла опустите перпендикуляр на другую сторону. Измерьте расстояние между концами перпендикуляра на сторонах угла, запишите результат измерения в числитель дроби. Теперь измерьте расстояние от вершины заданного угла до вершины прямого угла, т. е. до точки на стороне угла, в которую был опущен перпендикуляр. Полученное число запишите в знаменатель дроби. Составленная по результатам измерений дробь равна тангенсу угла.
Вычисление тангенса угла
Тангенс угла можно определить расчетным путем как отношение противолежащего ему катета к прилежащему. Также можно вычислить тангенс через прямые тригонометрические функции рассматриваемого угла — синус и косинус. Тангенс угла равен отношению синуса этого угла к его косинусу.
Особенности тангенса угла
В отличие от непрерывных функций синуса и косинуса, тангенс имеет разрыв и не определен при величине угла 90 градусов. При нулевом значении угла его тангенс равен нулю. Из соотношений прямоугольного треугольника очевидно, что угол 45 градусов имеет тангенс, равный единице, поскольку катеты такого прямоугольного треугольника равны.
Изменение тангенса угла
При значениях угла от 0 до 90 градусов его тангенс имеет положительное значение, поскольку синус и косинус в этом интервале положительны. Пределы изменения тангенса на этом участке - от нуля до бесконечно больших значений при углах, близких к прямому. При отрицательных значениях угла его тангенс также меняет знак.