Как найти точку пересечение двух линий
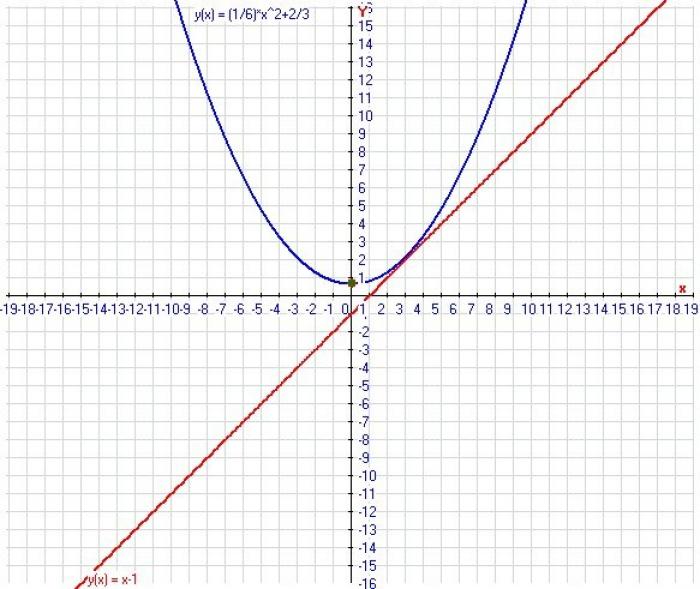
- Нахождение точки пересечения графиков
- Шаг 1: Запись уравнений линейных функций
- Шаг 2: Преобразование уравнений
- Шаг 3: Вычисление координат точки пересечения
- Пример
Нахождение точки пересечения графиков
На уроках математики школьники и студенты часто сталкиваются с линиями на координатной плоскости, которые представляют собой графики функций. Во многих алгебраических задачах требуется найти точку пересечения этих графиков. В данной статье мы рассмотрим алгоритм нахождения точки пересечения двух линейных функций.
Шаг 1: Запись уравнений линейных функций
Предположим, что у нас есть две линейные функции, представленные следующим образом: y₁=k₁x+b₁ и y₂=k₂x+b₂. Чтобы найти точку пересечения этих функций, необходимо решить уравнение k₁x+b₁=k₂x+b₂ или уравнение y₁=y₂.
Шаг 2: Преобразование уравнений
Преобразуем уравнение k₁x+b₁=k₂x+b₂ следующим образом: k₁x-k₂x=b₂-b₁. Затем выразим переменную x: x=(b₂-b₁)/(k₁-k₂). Таким образом, мы найдем значение x, то есть координату точки пересечения функций по оси абсцисс.
Шаг 3: Вычисление координат точки пересечения
Для вычисления соответствующей координаты по оси ординат, подставим найденное значение x в любую из функций. Таким образом, мы получим координаты точки пересечения (x, y), которые будут выглядеть следующим образом: ((b₂-b₁)/(k₁-k₂); k₁(b₂-b₁)/(k₁-k₂)+b₂).
Пример
Рассмотрим пример нахождения точки пересечения двух функций: f₂(x)=0,6x+1,2 и f₁(x)=0,5x². Приравняем эти функции и получим уравнение 0,5x²=0,6x+1,2. Перенесем все слагаемые в левую часть и решим полученное квадратное уравнение 0,5x² - 0,6x - 1,2=0. Правильным ответом будут значения x₁≈2,26 и x₂≈-1,06. Подставим эти значения в любую из функций и получим точки пересечения: т.А (2,26;2,55) и т.В (-1,06;0,56).
Исходя из рассмотренных примеров, вы сможете самостоятельно находить точки пересечения графиков различных функций. Знание основных алгоритмов позволит вам легко решать подобные задачи на уроках математики и не только.






