Как найти третью сторону треугольника, 2 стороны которого равны
- Вычисление длины основания равнобедренного треугольника
- Вычисление длины основания по координатам
- Вычисление длины основания при прямоугольном треугольнике
- Вычисление длины основания при заданном угле между боковыми сторонами
Вычисление длины основания равнобедренного треугольника
Наличие двух равных сторон в треугольнике позволяет назвать его равнобедренным, а эти стороны - боковыми. Если они заданы координатами в двух- или трехмерной ортогональной системе, вычисление длины третьей стороны - основания - сведется к нахождению длины отрезка по его координатам.
Вычисление длины основания по координатам
Если в исходных данных заданы координаты, определяющие боковые стороны, нет необходимости вычислять их длины или углы фигуры. Для вычисления размеров основания равнобедренного треугольника, рассмотрите отрезок между двумя несовпадающими точками - они определяют координаты основания. Далее, чтобы найти длину основания, найдите разницу между координатами вдоль каждой из осей, возведите ее в квадрат, сложите два (для двухмерного пространства) или три (для трехмерного) полученных значения и извлеките из результата квадратный корень.
Например, если сторона AB задана координатами точек A(3;5) и B(10;12), а сторона BC координатами точек B(10;12) и С(17;5), рассматривать нужно отрезок между точками A и C. Его длина составит AC = √((3-17)²+(5-5)²) = √((-14)² + 0²) = √196 = 14.
Вычисление длины основания при прямоугольном треугольнике
Если треугольник помимо равных сторон также является прямоугольным, то известен третий параметр - величина угла между боковыми сторонами. Угол в 90° не может не лежать между боковыми сторонами, так как в прямоугольном треугольнике к основанию (гипотенузе) всегда прилегают только острые (меньшие 90°) углы. Для вычисления длины третьей стороны в этом случае просто умножьте длину боковой стороны - катета - на корень из двойки: b = a*√2. Эта формула вытекает из теоремы Пифагора: квадрат гипотенузы (в случае равнобедренного треугольника - основания) равен сумме квадратов катетов (боковых сторон).
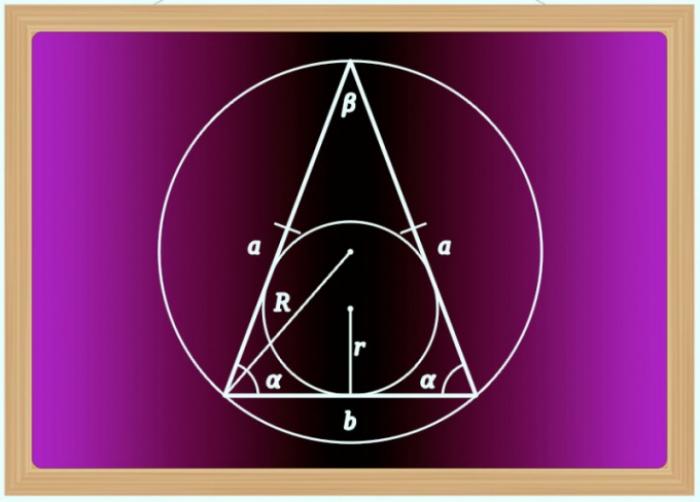
Вычисление длины основания при заданном угле между боковыми сторонами
Если угол между боковыми сторонами отличается от прямого и его величина дана в условиях вместе с длинами этих сторон, можно использовать теорему косинусов для нахождения длины основания. Применительно к равнобедренному треугольнику, равенство можно преобразовать таким образом: b² = a² + a² - 2*a*a*cos(β) = 2*a² - 2*a²*cos(β) = 2*a²*(1-cos(β)) = 2*a²*sin(β). Тогда окончательную формулу расчетов можно записать так: b = a*√(2*sin(β)).






