Как найти угловой коэффициент касательной к графику функции
- Как найти угловой коэффициент касательной к графику функции
- Получение углового коэффициента
- Производная функции и наличие касательной
- Пример решения
- Построение дополнительных касательных
Как найти угловой коэффициент касательной к графику функции
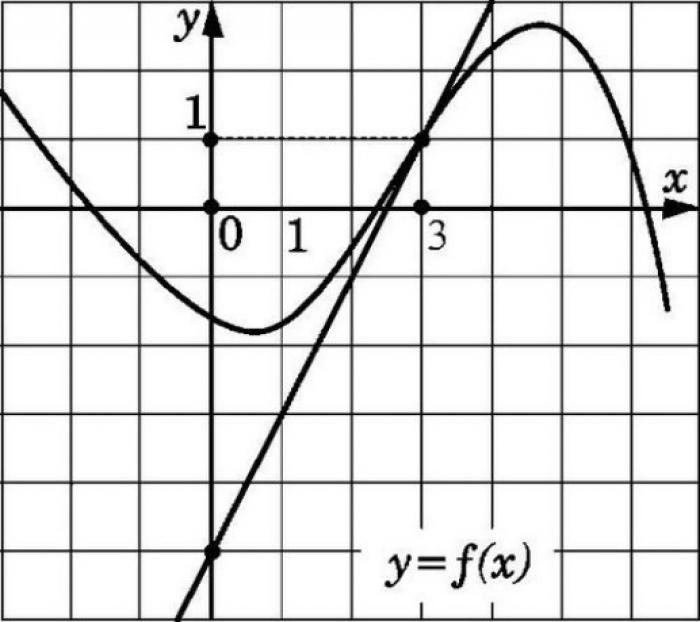
Для того чтобы найти угловой коэффициент касательной к графику функции, необходимо знать значение производной функции в точке касания.
Получение углового коэффициента
Представим график дифференцируемой функции f(x) в точке х0 как отрезок касательной. Этот отрезок будет достаточно близким к отрезку, проходящему через точки (х0; f(х0)) и (х0+Δx; f(x0 + Δx)). Для задания прямой, проходящей через точку А с координатами (х0; f(х0)), необходимо указать ее угловой коэффициент. Угловой коэффициент секущей касательной (при Δx→0) равен Δy/Δx и стремится к значению производной f'(x0).
Производная функции и наличие касательной
Если значение производной функции f'(x0) не существует, то возможно, что касательная отсутствует или проходит вертикально. В случае существования невертикальной касательной, она соприкасается с графиком функции в точке (х0, f(х0)). Угловой коэффициент данной касательной равен f'(х0). Таким образом, производная функции имеет геометрический смысл - расчет углового коэффициента касательной.
Пример решения
Для нахождения углового коэффициента касательной к графику функции у = х³ в точке с абсциссой Х0 = 1, необходимо найти производную данной функции и подставить значение абсциссы в производную. Производная функции у'(х) = 3х², поэтому у'(1) = 3 × 1² = 3. Таким образом, угловой коэффициент касательной в точке Х0 = 1 равен 3.
Построение дополнительных касательных
Для построения дополнительных касательных, соприкасающихся с графиком функции в точках x1, x2 и x3, необходимо отметить углы, которые образуются данными касательными с осью абсцисс. Угол α1 будет острым, угол α2 – тупым, а угол α3 будет равен нулю, так как проведенная касательная является параллельной оси ОХ. При этом тангенс тупого угла будет отрицательным, а тангенс острого угла – положительным, в случае tg0 результат будет равен нулю.






