Как найти углы равнобедренной трапеции
- Трапеция и ее особенности
- Вычисление углов равнобедренной трапеции
- Вычисление острого угла трапеции
- Вычисление углов при известной высоте трапеции
Трапеция и ее особенности
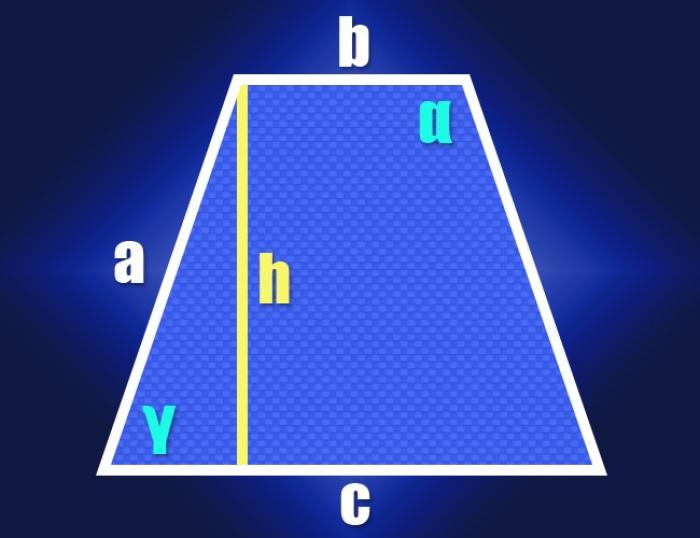
Трапеция - это плоская четырехугольная геометрическая фигура с обязательной параллельностью одной пары несоприкасающихся сторон. Основания трапеции - это пара параллельных сторон, а боковые стороны - это оставшиеся две стороны. Если длины боковых сторон трапеции одинаковы, то она называется равнобокой или равнобедренной. Формулы для вычисления углов равнобедренной трапеции могут быть получены из свойств прямоугольного треугольника.
Вычисление углов равнобедренной трапеции
Если известны длины обоих оснований (b и c) и одинаковых боковых сторон (a) равнобедренной трапеции, то можно использовать свойства прямоугольного треугольника для вычисления величины одного из ее острых углов (γ). Для этого нужно опустить высоту из любого угла, прилегающего к короткому основанию. Возникающий прямоугольный треугольник будет состоять из высоты (катет), боковой стороны (гипотенуза) и отрезка длинного основания между высотой и ближней боковой стороной (второй катет). Длину этого отрезка можно найти, вычтя из длины большего основания длину меньшего и разделив результат пополам: (c-b)/2.
Вычисление острого угла трапеции
После получения значений длин двух смежных сторон прямоугольного треугольника, можно перейти к вычислению угла между ними. Отношение длины гипотенузы (a) к длине катета ((c-b)/2) дает значение косинуса этого угла (cos(γ)), а функция арккосинус позволяет преобразовать его в величину угла в градусах: γ=arccos(2*a/(c-b)). Таким образом, можно получить величину одного из острых углов трапеции, а так как она равнобедренна, то второй острый угол будет иметь такую же величину. Сумма всех углов четырехугольника должна составлять 360°, поэтому сумма двух тупых углов будет равна разности между этим числом и двойным значением острого угла. Так как оба тупых угла также одинаковы, то для нахождения величины каждого из них (α) нужно разность разделить пополам: α = (360°-2*γ)/2 = 180°-arccos(2*a/(c-b)). Теперь у нас есть формулы для вычисления всех углов равнобедренной трапеции по известным длинам ее сторон.
Вычисление углов при известной высоте трапеции
Если длины боковых сторон трапеции неизвестны, но дана ее высота (h), то можно использовать такую же схему. В прямоугольном треугольнике, составленном из высоты, боковой стороны и короткого отрезка длинного основания, мы знаем длины двух катетов. Их соотношение определяет тангенс нужного нам угла, и эта тригонометрическая функция также имеет обратную функцию, преобразующую значение тангенса в величину угла - арктангенс. Полученные ранее формулы для острого и тупого углов трансформируются соответствующим образом: γ=arctg(2*h/(c-b)) и α = 180°-arctg(2*h/(c-b)).
Теперь у нас есть инструкции и формулы для вычисления углов равнобедренной трапеции в различных ситуациях. Эти знания могут быть полезны при решении геометрических задач и расчетах.