Как найти угол в трапеции
- Трапеция: определение и свойства
- Нахождение произвольного угла в трапеции
- Нахождение углов при равных сторонах трапеции
Трапеция: определение и свойства
Трапеция - это плоский четырехугольник, у которого две противолежащие стороны параллельны. Они называются основаниями трапеции, а две другие стороны - боковыми сторонами трапеции.
Нахождение произвольного угла в трапеции
Задача нахождения произвольного угла в трапеции требует достаточного количества дополнительных данных. Рассмотрим пример, в котором известны два угла при основании трапеции. Пусть известны углы ∠BAD и ∠CDA, найдем углы ∠ABC и ∠BCD.
Трапеция обладает таким свойством, что сумма углов при каждой боковой стороне равна 180°. Тогда ∠ABC = 180°-∠BAD, а ∠BCD = 180°-∠CDA.
Нахождение углов при равных сторонах трапеции
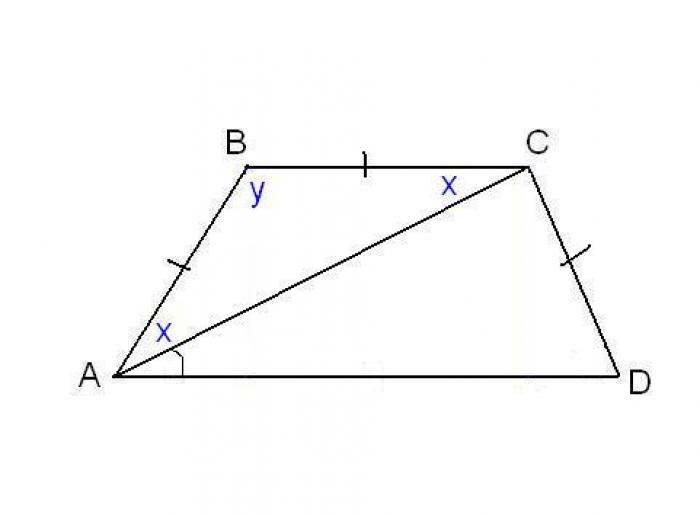
В другой задаче может быть указано равенство сторон трапеции и какие-нибудь дополнительные углы. Например, может быть известно, что стороны AB, BC и CD равны, а диагональ составляет с нижним основанием угол ∠CAD = α.
Рассмотрим треугольник ABC, он равнобедренный, так как AB = BC. Тогда ∠BAC = ∠BCA. Обозначим его x для краткости, а ∠ABC - y. Сумма углов любого треугольника равна 180°, из этого следует, что 2x + y = 180°, тогда y = 180° - 2x.
В то же время из свойств трапеции: y + x + α = 180° и следовательно 180° - 2x + x + α = 180°. Таким образом, x = α. Мы нашли два угла трапеции: ∠BAC = 2x = 2α и ∠ABC = y = 180° - 2α.
Так как AB = CD по условию, то трапеция равнобокая или равнобедренная. Значит, диагонали равны и равны углы при основаниях. Таким образом, ∠CDA = 2α, а ∠BCD = 180° - 2α.